Сила давления жидкости на криволинейные поверхности.

Рис.2.9.

Нахождение силы давления жидкости на криволинейные поверхности состоит в определении составляющих силы давления по нескольким направлениям с последующим геометрическим сложением этих сил.

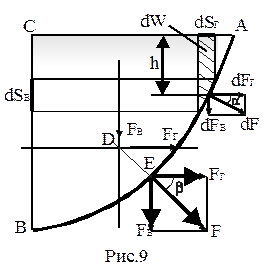
Рассмотрим цилиндрическую поверхность АВ, подверженную действию гидростатического давления. Выделим на этой поверхности бесконечно малую площадку dS, центр тяжести которой погружен на глубину h. На эту площадку нормально к цилиндрической поверхности будет действовать сила избыточного давления 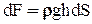, которую можно разложить на горизонтальную 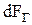и вертикальную 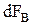составляющие. Предположим, что равнодействующая элементарная сила наклонена к горизонту под углом 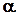. Тогда выражения для составляющих запишутся: 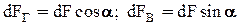. Подставив значение силы dF в выражение горизонтальной составляющей, получим 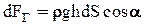. Из рисунка видно, что 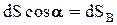это проекция элементарной площадки dS на вертикальную плоскость, следовательно 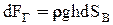. Тогда горизонтальная составляющая полной силы избыточного гидростатического давления равна:

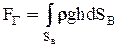Интеграл 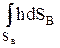является статическим моментом всей площади вертикальной проекции цилиндрической поверхности 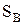относительно свободной поверхности жидкости, и этот статический момент равен произведению площади вертикальной проекции цилиндрической поверхности 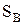на глубину погружения центра ее тяжести 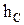, т.е. .

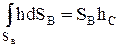Таким образом:

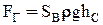; (2-15),

т.е. горизонтальная составляющая избыточного гидростатического давления, действующего на цилиндрическую поверхность, равна силе гидростатического давления, под воздействием которого находится вертикальная стенка, равная по площади вертикальной проекции рассматриваемой цилиндрической поверхности.

Определим вертикальную составляющую элементарной силы гидростатического давления 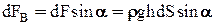. Величина 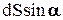является площадью 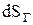проекции элементарной площадки dS на горизонтальную плоскость. Очевидно, что выражение 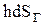представляет собой объем dW призмы (на рис. заштрихована). Произведение 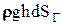является весом жидкости в этом бесконечно малом объеме, т.е. 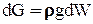. Вертикальная составляющая полной силы избыточного гидростатического давления равна:

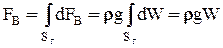; (2-16).

Объем W, являющийся суммой элементарных объемов dW, называется телом давления. Тело давления - это объем, заключенный между криволинейной поверхностью АВ, ее проекцией на свободную поверхность жидкости АС и вертикальной плоскостью проецирования. Вертикальная составляющая полной силы избыточного гидростатического давления на цилиндрическую поверхность равна весу жидкости в объеме тела давления.

Полная сила избыточного гидростатического давления определится 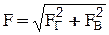; а ее направление - углом .

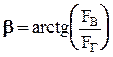Вектор полной силы давления F должен проходить через точку пересечения ее горизонтальной и вертикальной составляющих под углом 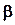. Линия действия силы 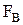проходит через центр тяжести тела давления, а линия действия силы 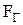проходит через центр давления вертикальной проекции криволинейной поверхности стенки. Из точки пересечения линий действия 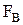и 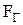(т. Д) проводится линия действия равнодействующей силы F под углом b и центр приложения полной силы давления на криволинейную поверхность будет на самой стенке (т. Е).

Закон Архимеда.

Рис.2.10.

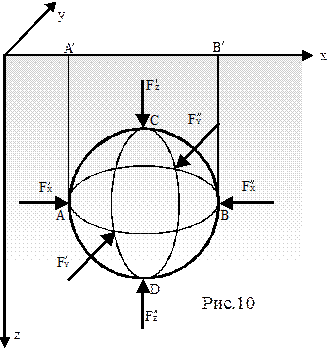
Допустим, что в жидкость погружено тело сферической формы. Со стороны жидкости на тело действуют силы 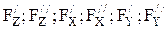. Очевидно, что силы 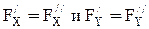, т.е. равны по величине и противоположны по направлению. Поэтому эти силы можно исключить из дальнейшего рассмотрения. Проведем линии 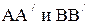, а тело разделим на две части плоскостью АВ. На. верхнюю часть тела жидкость воздействует с силой 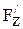, а на нижнюю 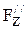. Результирующая сила равна .

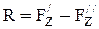Сила .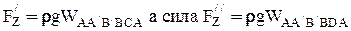

Отсюда 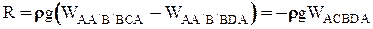. Эта формула выражает закон Архимеда, согласно которому сила, с которой жидкость воздействует на погруженное в нее тело, равна весу жидкости в объеме погруженного тела.