Уравнение неразрывности потока.

Рис.2.16.

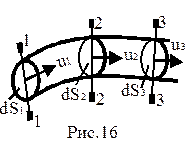
Вначале выведем уравнение неразрывности для струйки. Рассмотрим (рис.2.16.) отсек жидкости между сечениями 1-1 и 2-2 элементарной струйки. За время dt в отсек 1-2 через площадь живого сечения dS₁ втечет жидкость в количестве dS₁u₁dt (т.е. объем бесконечного малого цилиндра, имеющего основание dS₁ и длину u₁dt). За это же время через живое сечение dS₂ из отсека 1-2 вытечет объем жидкости dS₂u₂dt. При этом форма отсека не меняется (свойство “а” элементарной струйки), боковая поверхность непроницаема (свойство “б”) и жидкость несжимаема. Следовательно, объем жидкости, поступающий за время dt в отсек через сечение 1-1, должен быть равен объему жидкости, вытекающей за то же время из отсека через сечение 2-2:

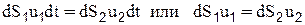
Аналогично и для других сечений, следовательно

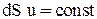(2-24)

уравнение неразрывности для элементарной струйки. Таким образом, расход жидкости во всех сечениях элементарной струйки одинаков (в данный момент времени). На основании уравнения (2-20) можно заключить, что скорости движения жидкости обратно пропорциональны площадям соответствующих живых сечений: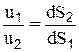

Рассмотрим участок потока (рис.2.14.). Возьмем несколько сечений 1-1, 2-2, 3-3. Обозначим S₁, S₂, S₃ и dS₁, dS₂, dS₃ площади живых сечений потока и площади живых сечений элементарной струйки в указанных сечениях, соответственно. Интегрируя выражение (2-24) в пределах соответствующих сечений, получим:

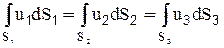. На основании зависимости (2-18) можно записать 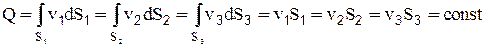; (2-25)

где v₁, v₂, v₃ - значения средних скоростей в сечениях 1-1, 2-2, 3-3. Уравнение (2-26) является уравнением неразрывности (сплошности) для целого потока жидкости при установившемся движении.

Аналогично (2-25) для целого потока можно записать: 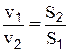. При установившемся движении произведения площади живого сечения потока на среднюю скорость есть величина постоянная, причем средние скорости потока обратно пропорциональны площадям соответствующих живых сечений.