Численное интегрирование.
S= 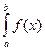 .Разобьем отрезок [a,b] на n равных частей.
.Разобьем отрезок [a,b] на n равных частей. 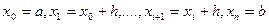
Обозначим: 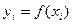
Заменим y=f(x) …… кусочно-полиномиальной функцией S(x) аппроксимирующей данную функцию. Интегрируя S(x) на отрезке [a,b], получим формулу численного интегрирования – квадратную формулу.
1)если на каждом интервале [ 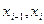 ] (i=1,2,…,n.) заменим f(x) ступенчатой функцией
] (i=1,2,…,n.) заменим f(x) ступенчатой функцией
f(x) 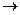 S(x) =
S(x) = 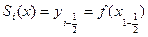 ,
, 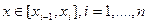
где 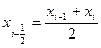 - середина интервала
- середина интервала 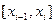
 тогда
тогда 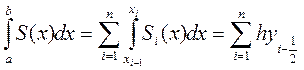 т.к
т.к 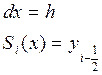
и получаем квадратурную формулу прямоугольников:
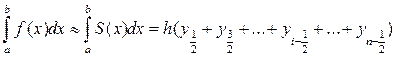 (1)
(1)
2)Если f(x) на каждом отрезке [ 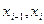 ] заменить её на линейной интерполяции по точкам
] заменить её на линейной интерполяции по точкам 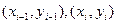 , то получим
, то получим
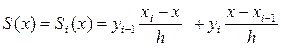
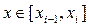 i=1,…,n
i=1,…,n 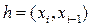
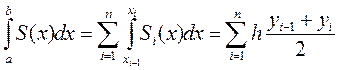 i=1,2,…..,n
i=1,2,…..,n
Действительно:
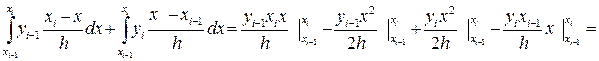
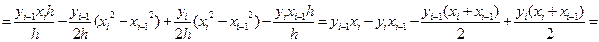
(т.к. 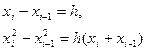 ) =
) = 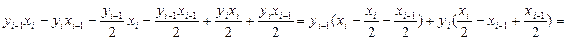
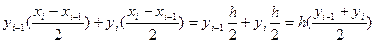
Т.о. получаем квадратурную формулу трапеций:
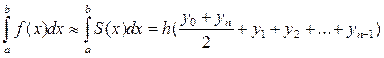 (2)
(2)
3) Если …. S(x) , определяет собой непрерывную функцию , составленную из примыкающих парабол, можно получить квадратурную формулу Симпсона, или формулу парабол.
Пусть на отрезке [ 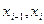 ] парабола проходит через точки (
] парабола проходит через точки ( 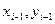 ),(
),( 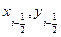 ),(
),( 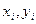 ) . Строим интерполяционный многочлен Лагранжа второго порядка:
) . Строим интерполяционный многочлен Лагранжа второго порядка:
(в знаменателе(первый шаг): 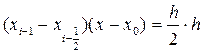 )
)
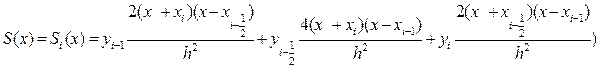
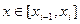 i=1,2,….,n
i=1,2,….,n
Введем новую переменную t : t = 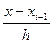 ;
;
Тогда 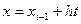 ;
; 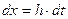 ;
;
Значениям t= 0, 1/2 , 1 соответствуют значения х ,равные 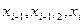 .
.
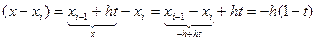 и т.д.
и т.д.
Выразим S(x) через новую переменную t:
S(x)= 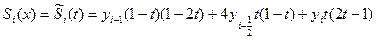 =
=
= 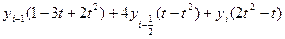 (i=1,2,….,n)
(i=1,2,….,n)
Рассмотрим, например, 1-ый член 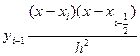
Т.к. 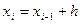 , а
, а 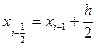 , получаем:
, получаем:
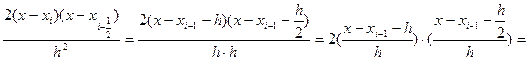
= 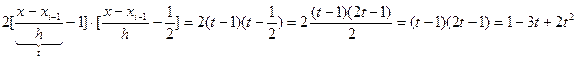
Далее, учитывая, что 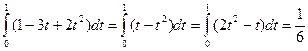 , получаем:
, получаем:
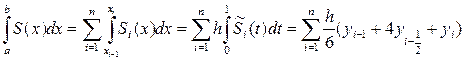
Т.о. имеем квадратурную формулу парабол:
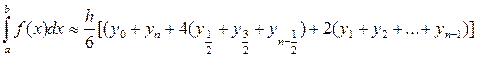 (3)
(3)
Погрешность каждой квадратичной формулы оценивается величиной остаточного члена R(h), зависящего от шага разбиения h (или от числа разбиений n):
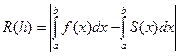
Если f(x) имеет непрерывную производную второго порядка , то получаем:
Для формулы трапеций
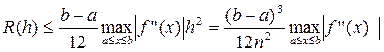
Если f(x) имеет непрерывную производную 4-го порядка, то оценка погрешности формулы Симпсона:
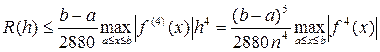
Пример:
Найти приближенное значение интеграла 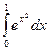 с помощью квадратурных формул прямоугольников , трапеций и Симпсона, если отрезок интегрирования [0,1] разбит на n =2; 4 ;10 равных частей. Оценить величину погрешности полученных результатов.
с помощью квадратурных формул прямоугольников , трапеций и Симпсона, если отрезок интегрирования [0,1] разбит на n =2; 4 ;10 равных частей. Оценить величину погрешности полученных результатов.
Решение:
Погрешность 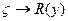 .
.
Находим производные f(x):
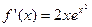 ;
; 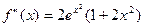 ;
; 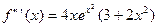 ;
; 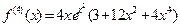
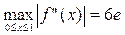 ;
; 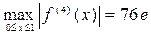
При n=4 получим:
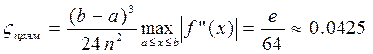 ;
;
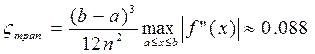
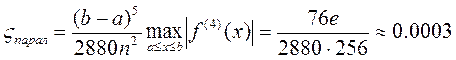 (в 200 раз точнее)
(в 200 раз точнее)
Результаты сведены в таблицу:
| формула | n=2 | n=4 | n=10 | |||
| Y (2) | 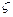
| Y (4) | 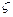
| Y (10) | 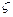
| |
| прямоугольник | 1.40977 | 0.1699 | 1.44875 | 0.0425 | 1.46039 | 0.0068 |
| трапеция | 1.57158 | 0.3398 | 1.49068 | 0.085 | 1.46717 | 0.0136 |
| Симпсона | 1.46371 | 0.0045 | 1.46272 | 0.0003 | 1.46265 | 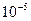
|
Дата добавления: 2016-11-04; просмотров: 2426;











