Первая интерполяционная формула Ньютона.

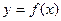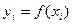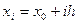
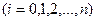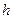Пусть для функции заданы значения для равноотстоящих узлов , где - шаг интерполяции.

Необходимо подобрать полином

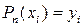
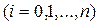(1)

Условия (1) эквивалентны тому, что

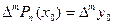, при .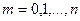

Следуя Ньютону, будем искать полином в виде

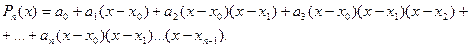(2)

Т.о. задача сводится к определению коэффициентов 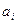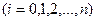в выражении (2).

Полагая 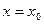, получим .

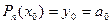Далее находим первую конечную разность 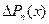и полагая 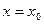, получим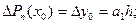

Откуда: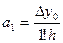

Беря затем вторые разности и т.д., получаем:

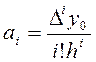
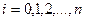
Введем в рассмотрение новую переменную

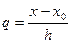- число шагов, необходимых для достижения точки 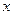из точки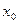

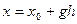( ), получим

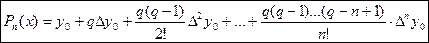(3)

первая интерполяционная формула Ньютона, которая применяется для интерполирования функций 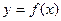, в окрестности начального значения 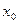, где q мало по абсолютной величине!

Если в (3) положить n=1, то получим формулу линейного интерполирования

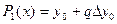(4)

При n=2 – формулу параболического или квадратичного интерполирования.

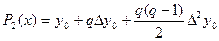
Если дана неограниченная таблица 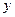, то n выбирают так, чтобы .

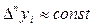Если таблица конечна, то n не может превышать k-1, где k – число строк таблицы.

При применении 1-ой интерполяционной формулы Ньютона удобно пользоваться горизонтальной таблицей разностей.

Пример: Построить на отрезке [3,5;3,7] интерполяционный полином Ньютона для функции 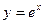, заданной таблицей, с шагом h=0,05.

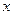
	3,50	3,55	3,60	3,65	3,70
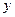
	33,115	34,813	36,598	38,475	40,447

Решение: составляем таблицу разностей

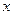
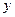
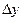
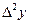
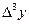
3,50 3,55 3,60 3,65 3,70	33,115 34,813 36,598 38,475 40,447	1,698 1,785 1,877 1,972	0,087 0,092 0,095	0,005 0,003

Т.к. 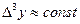то n=3.

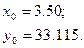
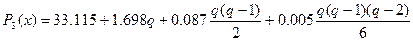или

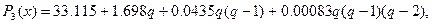
где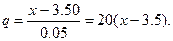

Можно упорядочить полином по степеням х, подставив значение q.

ЛЕКЦИЯ 9

Интерполирование функций. (Продолжение)