Конечно-разностные аппроксимации производных.

Пусть отрезок [а,b] разбит на n (n 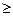2) равных частей.

Производные можно записывать с помощью конечных разностей:

а) разностей вперед: ;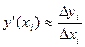

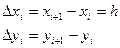
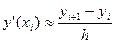( i=0,1,….,n-1) (1)

в) разностей назад (левые разности): 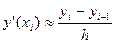; 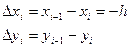(2)

c) центральных разностей: ;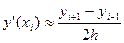

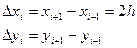
Приближенное значение производной второго порядка в точке х_{i :}

,

;

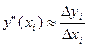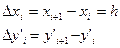
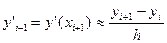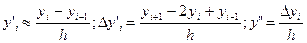
Т.о 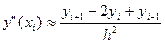i=1,2,…..n-1 (3)

Погрешность аппроксимации (3) имеет порядок 0 ( ).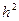

3. Использования интерполяционных многочленов Лагранжа для формул численного дифференцирования.

Функция у=f(x) на отрезке [a,b] разбитых на n равных интервалов, принимает значение в точках {x_i} (i=0,1,2….k)

y_i=f(x_i) ; b=x_n ; h=x_i-x_i-1=const.

Построим интерполяционный многочлен Лагранжа L_m(x) степень M:

L_m(x)=f(x _k)=y _k (k=i,i+1,….,i+m) i+m 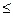n.

Многочлен L_m(x) интерполирует функцию f(x) на отрезке [x_i,x_i+m].

Дифференцируя L_m(x), получаем значение производных в точках {x_k} (k=i,i+1,…,i+m).

(Можно получить значения и в точках ,отличных от узлов.)

Если m=1 , то L₁(x)-линейная функция , график которой проходит через точки (х_i,y_i) и (х_i+1,y_i+1). Тогда

L₁(x)= 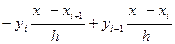; L₁’(x)=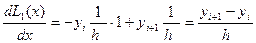

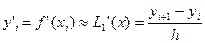
Если m=2, то график L₂(x) – парабола, проходящая через точки (х_i,y_i) , (х_i+1,y_i+1), (х_i+2,y_i+2).

L₂(x)=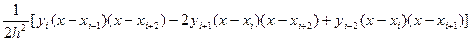

L₂’(x)= 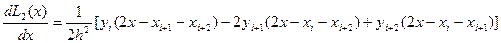(1)

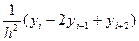L₂”(x)= (2)

Подставляя в (1) и (2) значения х, равные х_i,x_i+1,x_i+2:

Получим приближения производных f’(x) и f”(x) в этоих точках :

учитывая, что ;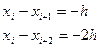

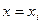
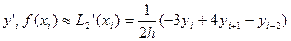
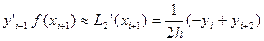(3)

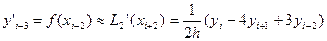
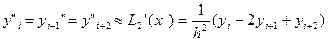(4)

Если функция f(x) имеет непрерывную производную до 3-го порядка включительно ,то

;

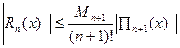
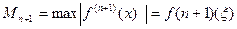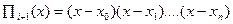
f(x) = L₂(x)+ R₂(x), (5)

где R₂(x)- остаточный член интерполяционной формулы.

R₂(x)=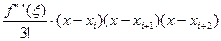

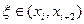
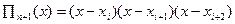
Дифференцируя (5) ,получим

f’(x) = L’₂(x)+ R’₂(x) (6)

f”(x) = L”₂(x)+ R”₂(x) (7)

Здесь,

R’₂(x)= 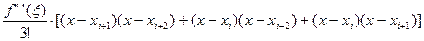; 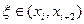(8)

Т.к. f”’( 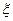)=const –дифференцируем по х.

R”₂(x)= ;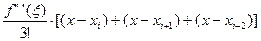

В точках х_i,x_i+1,x_i+2 (т.е. в узлах) получаем (подставляя значения х_i и т.д. в (8)-(9) и учитывая х_i-x_i+1=-h) :

R’₂(x_i)= 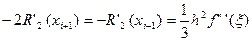(10)

R”₂(x_i)= 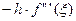, , 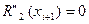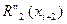= 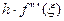(11)

Т.о. равенства (10) показывают, что погрешность аппроксимации первой производной f’(x) с помощью формулы (3) имеет один и тот же порядок 0(h²). (во всех трех точках.)

На отрезке [a,b] в точках х_i (i=0,1,2…,n) при n 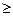2 рекомендуется применять следующие формулы:

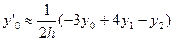i=0;

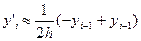(i=1,2,…,n-1); (12)

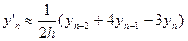i=n;

Погрешность аппроксимации второй производной имеет различный порядок в различных точках .(равенство(11)).Поэтому рекомендуется использовать многочлен Лагранжа третьей степени L³(x), имеющей 4 точки (узла) интерполяции. При этом погрешность во всех точках имеет один порядок h².

Рекомендуется формулы:

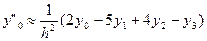i=0;

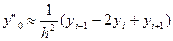( i=1,2,….,n-1);

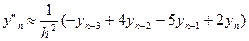i=n;

Пример:

Значение функции y=sin x заданы таблицей

Найти значения 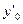и 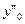и оценить погрешности вычислений.

Решение:

По формулам (3) или (12) получаем:

;

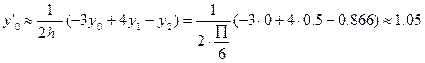По формуле (1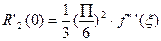0): 0< <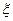

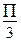
Т.к f(x)=sin x, то f”’(x)=-cos x.

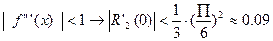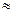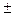. Т.о. y’₀ 1.05 0.09

По формуле (4)

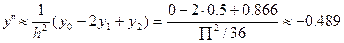
По формуле (11): 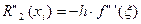получаем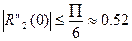

Т.о. y’₀ 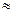-0.489 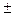0.52. Точность явно низкая.

y”₀=sin0=0

Следовало бы уменьшить шаг и увеличить число шагов. Затем использовать полином Лагранжа 4-ой степени и формулы (13).