Приближенное вычисление несобственных интегралов с бесконечными пределами.

Определение. Пусть f(x) непрерывна на промежутке [a,∞) и существует предел интеграла как функции верхнего предела интегрирования:

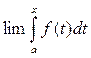(1)

х→∞

Тогда этот предел называется несобственным интегралом f(x) на промежутке [a,∞) обозначают так:

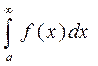
Если предел (1) существует, то несобственный интеграл сходиться на промежутке [а, ∞).

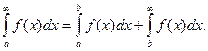(2)

Интеграл f(x) сходиться на [ a, ∞), если для любого ε >0, существует число в такое что

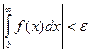(3)

Значение 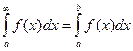с точностью ε

Пример: Дан сходящийся несобственный интеграл

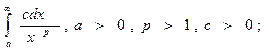
Используя условие (2) аппроксимировать его определенным интегралом с точностью ε. Осуществить замену переменной интегрирования так, чтобы верхний предел b был равен а+10.

Замена переменной имеет смысл, если условия (3) дает большой отрезок интегрирования!

Решение:

Т.к. f(x)>0, то условия (3) принимает вид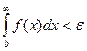

∞ ∞

Имеем = - =

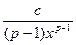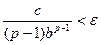
b b

Отсюда b> 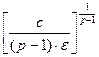(4)

В качестве b берем наименьшее целое, удовлетворяющее (4).

Если а=с=1, р=2,ε=0.001, то b >1000

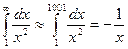То = 1 -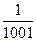

Точное значение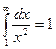

Погрешность не превышает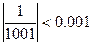

Вычислять интеграл 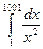приближенным (численными) методами сложно, т.к. b>>a.

Сделаем преобразование: x = t^m ; ;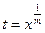

;

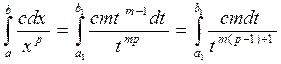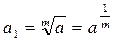
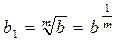
Показатель степени m полагаем равным ближайшему целому числу, не меньшему чем m=lg b/lg b₁

Нашем случае b=1001; b₁ = a+10 = 11 m = lg 1001/lg 11 ≈ 3

Сделав замену переменной x = t³, получаем =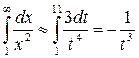

Рассмотренный интеграл можно считать эталонным, для многих интегралов. Рассмотрим, как используются эталонные интегралы на примере абсолютно сходящихся интегралов.

Не собственный интеграл функции 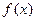на 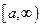называется абсолютно сходящимся, если несобственный интеграл абсолютной величины функции 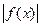на этом промежутке.

1. Если 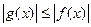для всех 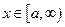если функция 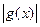эквивалентна 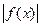при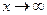

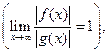и интеграл 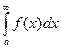сходится,

то сходится и интеграл .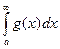

Условие (1) дает возможность использовать в неравенстве (3)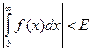

упрощенные подынтегральные функции вместо заданных.

Пример. Дан несобственный интеграл.

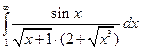
Аппроксимировать его определенным интегралом с точностью, не меньшей чем Е=0,001

Решение. 1. Упростим подынтегральную функцию.

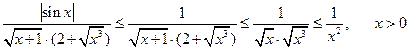
Воспользуемся неравенством (3) для оценки величины в:

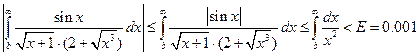
Из рассмотренного ниже примера:

b=1001; b₁=11 при замене .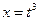

Тогда:

,

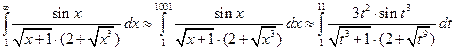с точностью не меньшей чем 0,001.

Приближенное значение несобственных интегралов от функции с бесконечным разрывом.

Пусть функция 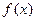непрерывна на промежутке 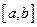и предел функции при x, стремящемся к b, равен бесконечности, т.е. не существует.

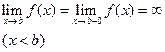(1)

Если предел 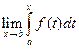существует, то интеграл несобственный.

Несобственный интеграл функции, имеющий бесконечный разрыв в некоторой внутренней точке 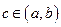определяют на 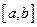, как сумму сходящихся интегралов на отрезках .

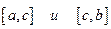Несобственные интегралы с бесконечным разрывом подынтегральной функции на отрезке интегрирования с помощью замены переменной интегрирования преобразуют к несобственным интегралам с бесконечными пределами.

Пример. Дан собственный интеграл 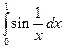. С помощью замены переменой преобразовать его в несобственный интеграл с бесконечным пределом.

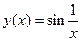функция не определена в точке x=0 (нижний предел интегрирования). Проведем замену так, чтобы особой точке соответствовала бесконечно удаленная.

Простейшая замена: 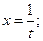при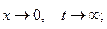

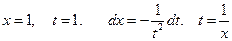
Тогда:

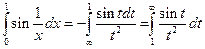
Для интеграла 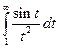можно получить его приближение (аналогично рассмотренному выше) на отрезке 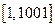с заданной точностью.

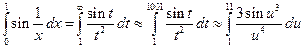
(последующее преобразование 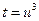уменьшает интервал интегрирования до )

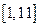ЛЕКЦИЯ 15