Нормированное нормальное распределение

Формула 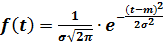описывает целое семейство нормальных кривых, зависящих, как было сказано выше, от двух параметров —m и σ, которые могут принимать любые значения, поэтому возможно бесконечно много нормально распределенных совокупностей.

Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая по достаточно сложной формуле, используют так называемое нормированное (или стандартное) нормальное распределение N(0;1), для которого составлены подробные таблицы.

Нормированное нормальное распределение имеет параметры m = 0 и

σ = 1. Это распределение получается, если пронормировать нормально распределенную величину X по формуле:

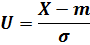
Плотность распределения вероятностей нормированного нормального распределения записывается в виде:

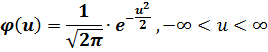
На кривой нормированного нормального распределения указаны в процентах доли площадей соответствующих отмеченным значениям нормированного отклонения и, по отношению к общей площади под кривой, равной 1 (100%). Эти площади определяют вероятности попадания случайной величины в соответствующие интервалы.

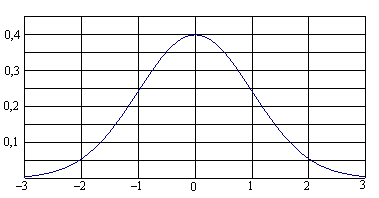
Рис. . График нормированного нормального распределения.

Таблица значений — ординат нормальной кривой приведена в специальных таблицах. Значения φ(u) для некоторых характерных нормированных отклонений представлены в табл.

Таблица . Ординаты нормальной кривой