Логарифмически нормальное (логнормальное) распределение.

При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины T, а не сама эта величина.

Логарифмически нормальное распределение во многом более точно, чем нормальное описывает наработку до отказа тех объектов, у которых отказ возникает вследствие усталости, например, подшипников качения, электронных ламп и пр.

Если величина lg t имеет нормальное распределение с параметрами:

математическое ожидание — U и среднее квадратичное отклонение V, то величина T считается логарифмически нормально распределенной с плотностью распределения, описываемой выражением:

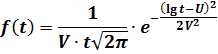
Параметры U и V по результатам испытаний принимаются:

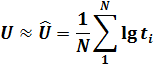
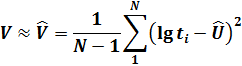
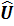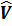где и - оценки параметров Uи V.

Графики изменения показателей надежности при логарифмически нормальном распределении приведены на рис. .

Числовые характеристики наработки до отказа:

- средняя наработка (математическое ожидание наработки) до отказа:

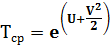
- дисперсия наработки до отказа:

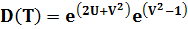
Рис. .. Графики изменения показателей надежности при логарифмически нормальном распределении.