Нормальное распределение.

Этот вид распределений занимает особое место и играет исключительно важную роль в теории вероятностей и теории надежности. Главная его особенность состоит в том, что нормальное распределение является предельным распределением, к которому приближаются другие законы распределения.

Можно показать, что сумма достаточно большого числа независимых (или слабозависимых) СВ, подчиненных каким угодно законам распределения. приближенно подчиняется нормальному закону распределения. причем тем точнее, чем большее количество СВ суммируется.

Основное ограничение, налагаемое на суммирование СВ, состоит в том, чтобы все величины в общей сумме имели относительно малое значение (к таким СВ относятся, например, ошибки измерения. ошибки методического порядка и т.п.). Если это условие не выполняется и одно из случайных значений резко превалирует в сумме над всеми другими, то это оказывает влияние на сумму и определяет в основном ее закон распределения.

Из сказанного следует, что в том случае, когда к появлению отказа приводит множество случайных факторов, причем каждый из них не вносит по сравнению с другими решающий вклад в развитие процессов, приводящих к отказу, то можно ожидать, что распределение времени безотказной работы будет нормальным. В частности, нормальному закону подчиняется наработка к возникновению отказов, вызванная механическим износом из-за трения.

В отличие от экспоненциального и распределения Вейбулла-Гнеденко, которые применимы только для положительных непрерывных СВ, нормальное распределение применимо для непрерывных СВ, которые могут принимать, как положительные, так и отрицательные значения от -∞ до +∞.

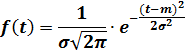
Где 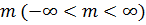— параметр сдвига; 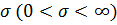— параметр масштаба.

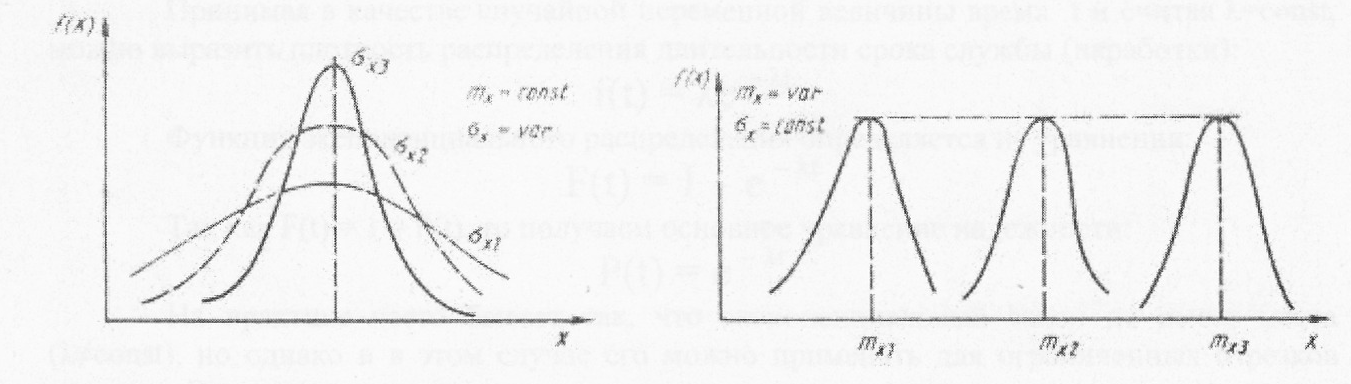
Рис. . Графики изменения плотности нормального распределения.

Функция нормального распределения выглядит следующим образом:

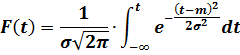
Среднее время безотказной работы:

T_ср = m

Дисперсия:

D(T) = σ²