Экспоненциальный закон распределения.

Экспоненциальный закон один из основных законов распределения длительности срока службы технических устройств. В частности, этому закону следует время наработки до отказа некоторых неремонтируемых изделий и наработка между отказами ремонтируемых изделий при их работе на установившихся режимах (для внезапных отказов, не связанных с износом или старением элементов изделия). Это распределение характерно также для отказа сложных систем, состоящих из однотипных деталей.

В качестве основного параметра экспоненциального распределения является интенсивность отказов λ(t) для неремонтируемых, и параметр потока отказов ω(t) — для ремонтируемых изделий. Для неремонтируемых изделий λ(t) показывает, какая доля работающих в момент времени изделий выходит из строя в единицу времени после момента t.

Принимая в качестве случайной переменной величины время и считая

λ = const можно выразить плотность распределения длительности срока службы (наработки):

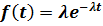
Функция экспоненциального распределения определяется из уравнения:

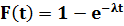
х

ех

Рис. . График экспоненциальной функции

Т.к. F(t)=1-P(t), основное уравнение надежности будет иметь вид:

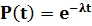
На практике часто бывает так, что экспоненциальный закон не имеет места (λ≠const), однако и в этом случае его можно применить для ограниченных отрезков времени.

Данное допущение оправдывается тем, что при ограниченном периоде времени переменную интенсивность отказов, без большой ошибки, можно заменить средним значением λ_ср, т.е.:

λ(t)~ λ_ср(t)

Среднее время безотказной работы:

T_cp = 1/λ.