Напівлогарифмічні моделі. Визначення темпів зростання.
Log-lin модель
Економісти, бізнесмени, урядовці часто стикаються з питанням визначення темпів зростання різних економічних показників, таких як населення, валовий національний продукт, грошова маса, зайнятість, продуктивність, торговий дефіцит і под.
У табл. 4.3 наведені дані про реальний валовий внутрішній продукт США за період 1972–1991 рр.
Таблиця 4.3
Валовий внутрішній продукт у поточних доларах і доларах 1987 р.
| Рік | ВВП, в поточ. млрд. дол. | ВВП, млрд. дол. 1978 р. |
| 1207,0 | 3107,1 | |
| 1349,6 | 3268,6 | |
| 1458,6 | 3248,1 | |
| 1585,9 | 3221,7 | |
| 1768,4 | 3380,8 | |
| 1974,1 | 3533,3 | |
| 2232,7 | 3703,5 | |
| 2488,6 | 3796,8 | |
| 2708,0 | 3776,3 | |
| 3030,6 | 3843,1 | |
| 3149,6 | 3760,3 | |
| 3405,0 | 3906,6 | |
| 3777,2 | 4148,5 | |
| Продовження табл. 4.3 | ||
| 4038,7 | 4279,8 | |
| 4268,6 | 4404,5 | |
| 4539,9 | 4539,9 | |
| 4900,4 | 4718,6 | |
| 5250,8 | 4838,0 | |
| 5522,2 | 4877,5 | |
| 5677,5 | 4821,0 |
Припустимо, ми хочемо визначити за цей період темпи зростання внутрішнього валового продукту. Позначимо через Yt реальний валовий внутрішній продукт у момент часу t, а Y0 – початкове (в 1972 р.) значення цієї змінної. Застосуємо добре відому формулу складних відсотків
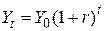 , ,
| (4.5.1) |
де r – складний відсоток приросту Y. Логарифмуючи обидві частини рівняння (4.5.1), одержуємо
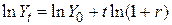 . .
| (4.5.2) |
Позначимо тепер
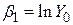 , ,
| (4.5.3) |
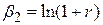 . .
| (4.5.4) |
Рівність (4.5.2) можна переписати у вигляді
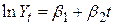 . .
| (4.5.5) |
Додаючи в (4.5.5) випадкову складову, одержуємо
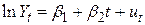 . .
| (4.5.6) |
Ця модель схожа на звичайну модель лінійної регресії. Єдина різниця полягає в тому, що регресант входить у рівняння як логарифм Y, а регресор, час t, набуває значення 1, 2, 3 і т.д.
Модель вигляду (4.5.6) називається напівлогарифмічною моделлю, оскільки одна зі змінних (у даному випадку регресант) входить у неї у вигляді логарифма. Подібну модель називають також log-lin моделлю. Пізніше ми розглянемо модель, у якій регресант входить лінійно, а регресор – у вигляді логарифма. Така модель називається lin-log-моделлю.
Перш ніж звернутися до результатів регресії, дослідимо властивості моделі (4.5.5). У цій моделі кутовий коефіцієнт визначає постійну відносну зміну Y для даної абсолютної зміни регресора (у даному випадку змінну t), тобто
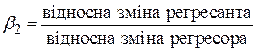 . .
| (4.5.7) |
Якщо помножити відносну зміну Y на 100, то (4.5.7) дасть нам процентну зміну або темп зростання Y для абсолютної зміни регресора Х.
Модель типу (4.5.5) є особливо корисною в разі, коли змінна Х - час, як у нашому випадку з валовим національним продуктом. У такому випадку модель визначає постійний ( 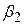 ) темп зростання (якщо
) темп зростання (якщо 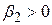 ) або зменшення (
) або зменшення ( 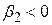 ) змінної Y. Тому ця модель ще називається моделлю постійного зростання.
) змінної Y. Тому ця модель ще називається моделлю постійного зростання.
Повертаючись, наприклад, до реального валового внутрішнього продукту, ми одержуємо такі результати:
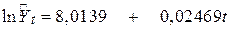 (0,0114) (0,00956)
(0,0114) (0,00956) 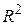 =0,9738
t = (700,54) (25,8643)
p = (0,0000) (0,0000) =0,9738
t = (700,54) (25,8643)
p = (0,0000) (0,0000)
| (4.5.8) |
Інтерпретація результатів. За період 1972–1991 рр. реальний валовий внутрішній продукт мав річний темп приросту 2,469%. Оскільки 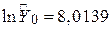 то
то 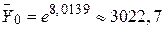 , тобто на початку 1972 р. оцінка реального внутрішнього валового продукту складала приблизно 3 023 млрд дол. Лінія регресії показана на рис. 4.4.
, тобто на початку 1972 р. оцінка реального внутрішнього валового продукту складала приблизно 3 023 млрд дол. Лінія регресії показана на рис. 4.4.
Кутовий коефіцієнт 0,02469, отриманий в (4.5.8), або в загальному випадку коефіцієнт  в моделі зростання (4.5.5) дає миттєвий (для даного моменту часу) темп зростання, а не складний (за даний період часу) відсоток приросту. Але останній можна легко отримати з рівняння (4.5.4). Оскільки
в моделі зростання (4.5.5) дає миттєвий (для даного моменту часу) темп зростання, а не складний (за даний період часу) відсоток приросту. Але останній можна легко отримати з рівняння (4.5.4). Оскільки  , то
, то 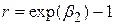 . Підставляючи сюди
. Підставляючи сюди 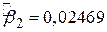 , отримуємо таке значення оцінки складного відсотка:
, отримуємо таке значення оцінки складного відсотка: 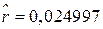 або близько 2,499%. Таким чином, за досліджуваний період складний відсоток темпів зростання валового внутрішнього продукту складає приблизно 2,499% на рік. Цей темп зростання трохи вищий, ніж миттєвий темп зростання 2,469%.
або близько 2,499%. Таким чином, за досліджуваний період складний відсоток темпів зростання валового внутрішнього продукту складає приблизно 2,499% на рік. Цей темп зростання трохи вищий, ніж миттєвий темп зростання 2,469%.
Модель лінійного тренда. Замість моделі (4.5.6) іноді застосовується модель
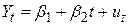 , ,
| (4.5.9) |
тобто замість використання в моделі регресії lnY ми використовуємо величину Y. Як регресор знову виступає час t. Така модель називається моделлю лінійного тренда, а час t - змінною тренда. Під трендом ми розуміємо безперервний приріст або спад у характері змінної. Якщо кутовий коефіцієнт в (4.5.9) позитивний, то ми говоримо про тенденцію до підвищення Y, а при негативному значенні – до пониження Y.
Для нашого прикладу про реальний ВВП модель (4.5.9) дає такі результати:
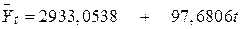 (50,5913) (4,2233)
(50,5913) (4,2233) 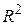 =0,9674
t = (57,9754) (23,1291)
p = (0,0000) (0,0000) =0,9674
t = (57,9754) (23,1291)
p = (0,0000) (0,0000)
| (4.5.10) |
Інтерпретація результатів. За період 1972–1991 рр. в середньому реальний ВВП зростав в абсолютному (не у відносному) значенні приблизно на 97,68 млрд дол. Таким чином, за цей період реальний ВВП мав тенденцію до зростання.
Вибір між моделями зростання (4.5.8) і лінійною моделлю тренда (4.5.10) залежить від того, що нас цікавить – абсолютні чи відносні зміни реального ВВП. Відзначимо, що здебільшого відносні зміни важливіші. Ще раз відзначимо, що ми не можемо порівнювати коефіцієнти детермінації моделей (4.5.8) і (4.5.10), оскільки регресанти в них різні.
Lin-Log модель. Припустимо, що у нас є дані, наведені в табл. 6.3, в якій Y – ВНП, а Х – грошова маса (М2= засоби грошового обігу + внески + депозити до запитання + дорожні чеки + інші чекові внески +...). Припустимо далі, що нас цікавить, наскільки (в абсолютному значенні) зростає ВНП, якщо грошова маса зростає, скажімо, на 1%.
На відміну від тільки що розглянутої моделі зростання, в якій нас цікавив відсоток зростання Y для абсолютної одиничної зміни Х, тепер нас цікавить абсолютна зміна Y для заданого відсотка зміни Х. Модель, що дозволяє виконати це завдання, така:
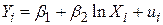 . .
| (4.5.11) |
Дану модель називають lin-log-моделлю. Пояснимо значення коефіцієнта 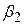 . Як завжди
. Як завжди
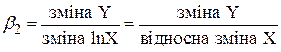 . .
|
Друга рівність базується на тому, що зміна логарифма величини дорівнює відносній зміні цієї величини.
У математичних символах це може бути записано у вигляді
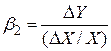 . .
| (4.5.12) |
Рівняння (4.5.12) можна записати і в еквівалентному вигляді
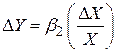 . .
| (4.5.13) |
Це рівняння говорить про те, що абсолютна зміна Y (тобто DY) дорівнює добутку 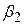 й відносної зміни Х. Якщо останнє (тобто DХ/X) помножити на 100, то (4.5.13) дасть абсолютну зміну Y для процентної зміни Х. Так, якщо DХ/X зміниться на 0,01 (або 1%), то абсолютна зміна Y буде дорівнювати 0,011
й відносної зміни Х. Якщо останнє (тобто DХ/X) помножити на 100, то (4.5.13) дасть абсолютну зміну Y для процентної зміни Х. Так, якщо DХ/X зміниться на 0,01 (або 1%), то абсолютна зміна Y буде дорівнювати 0,011 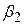 . Таким чином, якщо при розв’язанні задачі регресії знайдено
. Таким чином, якщо при розв’язанні задачі регресії знайдено 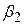 =500, то абсолютна зміна Y дорівнює 0,01´500 або 5. Отже, при використовуванні моделі регресії (4.5.11) після знаходження за МНК кутового коефіцієнта
=500, то абсолютна зміна Y дорівнює 0,01´500 або 5. Отже, при використовуванні моделі регресії (4.5.11) після знаходження за МНК кутового коефіцієнта 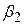 для визначення абсолютної зміни Y при зміні Х на 1% необхідно
для визначення абсолютної зміни Y при зміні Х на 1% необхідно 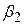 помножити на 0,01.
помножити на 0,01.
Таблиця 4.4
ВНП і грошова маса в США, 1973–1987 рр.
| Рік | ВНП, млрд дол. | Грошова маса, млрд дол. |
| 1359,3 | 861,0 | |
| 1472,8 | 908,5 | |
| 1598,4 | 1023,2 | |
| 1782,8 | 1163,7 | |
| 1990,5 | 13286,7 | |
| 2249,7 | 1389,0 | |
| 2508,2 | 1500,2 | |
| 2723,0 | 1633,1 | |
| 3052,6 | 1795,5 | |
| 3166,0 | 1954,5 | |
| 3405,7 | 2185,2 | |
| 3772,2 | 2363,6 | |
| 4014,4 | 2562,6 | |
| 4240,3 | 2807,7 | |
| 4526,7 | 2901,0 |
Використовуючи дані, наведені в табл. 4.4, можна отримати такі результати:
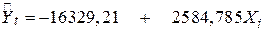 (696,599) (94,041)
(696,599) (94,041) 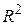 =0,9831
t = (–23.441) (27.486)
p = (0.0000) (0.0000) =0,9831
t = (–23.441) (27.486)
p = (0.0000) (0.0000)
| (4.5.14) |
Інтерпретація результатів. Значення кутового коефіцієнта 2584,785 означає, що за даний період збільшення грошової маси на 1% призводило, в середньому, до зростання ВНП приблизно на 25,85 млрд дол. (2585´0,01=25,85).
Обернені моделі
Під оберненими моделями розуміють моделі такого вигляду:
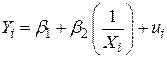 . .
| (4.6.1) |
Ця модель, як і вищерозглянуті, є лінійною щодо регресора Х, а також лінійна щодо коефіцієнтів регресії 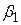 і
і 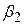 .
.
У оберненої моделі (4.6.1) є одна відмінна риса. При необмеженому зростанні змінної Х складова 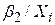 прямує до нуля, а регресант
прямує до нуля, а регресант 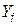 асимптотично наближається до величини
асимптотично наближається до величини 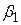 . Таким чином, модель (4.6.1) містить асимптотичний параметр, до якого прямує залежна змінна Y при необмеженому зростанні змінної Х.
. Таким чином, модель (4.6.1) містить асимптотичний параметр, до якого прямує залежна змінна Y при необмеженому зростанні змінної Х.
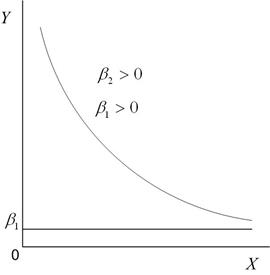
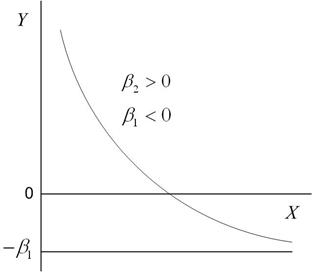
а б
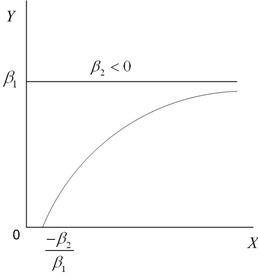
в
Рис. 4.4 Приклади графіків обернених моделей: а - моделі (4.6.1);
б - кривої Філіпса; в - кривої Енгеля
На рис. 4.4 зображені характерні криві оберненої моделі залежно від знаків коефіцієнтів регресії.
Одним із важливих додатків моделі (рис. 4.4, б) є відома з макроекономіки крива Філіпса. На підставі даних про темпи зростання заробітної плати (Y) і процента зміни рівня безробіття (Х) для Великобританії в період з 1861 по 1957 рр. Філіпс отримав криву вигляду рис. 4.4, б, яка детально зображена на рис.4.5.
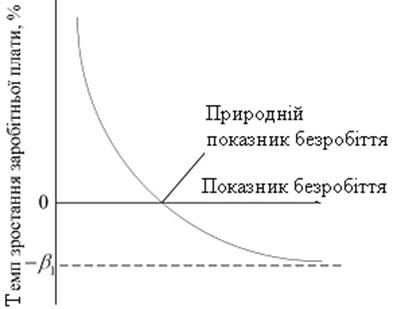
Рис. 4.5. Крива Філіпса
З рис. 4.5 бачимо, що є асиметрія в залежності темпів зростання заробітної плати від рівня безробіття: заробітна плата зростає швидше при рівні безробіття, меншому величини UN (natural rate unemployment), який називається природним рівнем безробіття. При рівні безробіття, більшому за цю величину, зменшення темпів зростання зарплати стає більш плавним. При необмеженому збільшенні рівня безробіття темпи зростання зарплати наближаються до асимптотичного значення.
Важливим додатком залежності вигляду (4.6.1) є крива витрат Енгеля, що характеризує зв’язок витрат споживача на товар із його загальними витратами або доходом. Якщо позначити через Y витрати на товар, а через Х – дохід споживача, то певні товари матимуть такі властивості. Існує деякий критичний або пороговий рівень доходу, нижче якого товар не купується. На рис. 4.4, в цей рівень має значення 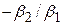 . Існує рівень насичення товару, вище цього рівня споживання товару не відбувається, яким би високим не був рівень доходу. Цей рівень у моделі (4.6.1) визначається асимптотою
. Існує рівень насичення товару, вище цього рівня споживання товару не відбувається, яким би високим не був рівень доходу. Цей рівень у моделі (4.6.1) визначається асимптотою 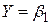 . Для таких товарів найбільш відповідною є модель, подана на рис. 4.4, в.
. Для таких товарів найбільш відповідною є модель, подана на рис. 4.4, в.
Дата добавления: 2016-07-27; просмотров: 1738;











