Ілюстративний приклад. Попит на каву
Провівши обчислення за даними, наведеними в таблиці, одержуємо такий результат:
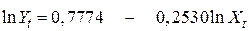 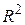 =0,7448
(0,0152) (0,0494) =0,7448
(0,0152) (0,0494) 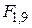 = 26,27
t = (51,0045) (–5,1251) = 26,27
t = (51,0045) (–5,1251)
| (4.4.5) |
де Yt – попит на каву (кількість випитих чашок кави за день), а Xt – ціна на каву в доларах за фунт кави.
З цих результатів ми бачимо, що коефіцієнт еластичності ціни дорівнює –0,25. Це значить, що при зростанні на 1% реальної ціни за фунт кави, попит на неї зменшиться в середньому на 0,25%. Оскільки еластичність ціни менше 1 за абсолютною величиною, ми можемо сказати, що попит на каву нееластичний за ціною.
Цікавим є наступне питання. Чи можемо ми визначити, яка з моделей є кращою, порівнюючи результати лінійної та лінійно-логарифмічної функції попиту? Чи можемо ми сказати, що (4.4.5) краще, ніж (3.7.1), оскільки її 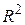 вище (0,7448 проти 0,6628)? На жаль, ми не можемо зробити такий висновок, оскільки в тому випадку, коли залежна змінна у двох моделях неоднакова (тут Y і lnY), коефіцієнти детермінації безпосередньо порівнювати не можна. Ми не можемо порівнювати два кутових коефіцієнти ще й з іншої причини. Для моделі (3.7.1) кутовий коефіцієнт дає ефект одиничної зміни ціни на каву, скажемо на 1 дол. за фунт, на постійну абсолютну величину зменшення споживання, що складає 0,4795 чашки кави за день. З іншого боку, коефіцієнт –0,2530, отриманий в (4.4.5), дає постійне процентне зменшення споживання кави в результаті 1%-го зростання ціни на каву за фунт, тобто дає еластичність ціни.
вище (0,7448 проти 0,6628)? На жаль, ми не можемо зробити такий висновок, оскільки в тому випадку, коли залежна змінна у двох моделях неоднакова (тут Y і lnY), коефіцієнти детермінації безпосередньо порівнювати не можна. Ми не можемо порівнювати два кутових коефіцієнти ще й з іншої причини. Для моделі (3.7.1) кутовий коефіцієнт дає ефект одиничної зміни ціни на каву, скажемо на 1 дол. за фунт, на постійну абсолютну величину зменшення споживання, що складає 0,4795 чашки кави за день. З іншого боку, коефіцієнт –0,2530, отриманий в (4.4.5), дає постійне процентне зменшення споживання кави в результаті 1%-го зростання ціни на каву за фунт, тобто дає еластичність ціни.
Чи можна порівняти результати двох використаних моделей? Одним із шляхів порівняння двох моделей є наближене визначення еластичності ціни для моделі (2.7.1). Це може бути зроблено таким чином.
Еластичність Е змінної Y по відношенню до іншої змінної Х визначається за формулою:
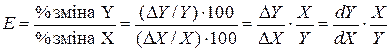 . .
| (4.4.6) |
Для лінійної моделі (2.7.1) оцінка кутового коефіцієнта  дорівнює –0,4795. Як показано в (4.4.6), для знаходження еластичності необхідно помножити кутовий коефіцієнт
дорівнює –0,4795. Як показано в (4.4.6), для знаходження еластичності необхідно помножити кутовий коефіцієнт 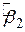 на відношення Х/Y (ціни до кількості). Але які величини Х і Y повинні ми вибрати? Звичайно, ми можемо підрахувати еластичність для кожної з 11 пар значень Х і Y. На практиці, проте, еластичність підраховується в середніх значеннях Х і Y. Ми одержуємо оцінку середньої еластичності. Для нашого прикладу
на відношення Х/Y (ціни до кількості). Але які величини Х і Y повинні ми вибрати? Звичайно, ми можемо підрахувати еластичність для кожної з 11 пар значень Х і Y. На практиці, проте, еластичність підраховується в середніх значеннях Х і Y. Ми одержуємо оцінку середньої еластичності. Для нашого прикладу 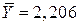 чашки і
чашки і 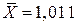 дол. Використовуючи ці величини і
дол. Використовуючи ці величини і 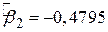 , одержуємо з (4.4.6) середню еластичність –0,2197 або наближено –0,22. Цей результат отриманий із лінійної моделі й відрізняється від коефіцієнта еластичності –0,25, отриманого в лінійній логарифмічній моделі. Зазначимо, що цей коефіцієнт еластичності є постійним у всіх точках Х, тоді як у лінійній моделі коефіцієнт еластичності змінюється від точки до точки.
, одержуємо з (4.4.6) середню еластичність –0,2197 або наближено –0,22. Цей результат отриманий із лінійної моделі й відрізняється від коефіцієнта еластичності –0,25, отриманого в лінійній логарифмічній моделі. Зазначимо, що цей коефіцієнт еластичності є постійним у всіх точках Х, тоді як у лінійній моделі коефіцієнт еластичності змінюється від точки до точки.
Дата добавления: 2016-07-27; просмотров: 1855;











