ВИЗНАЧЕННЯ ІНДУКТИВНОСТІ СОЛЕНОЇДА ТА ЄМНОСТІ КОНДЕНСАТОРА МЕТОДОМ ВИМІРЮВАННЯ ЇХ РЕАКТИВНИХ ОПОРІВ У КОЛІ ЗМІННОГО СТРУМУ

Змінний електричний струм – це струм, який змінюється за величиною і напрямом. Наприклад, ця зміна може відбуватись за гармонічним законом

I = I_osin(wt+j₀), (54.1)

де І_o - максимальне (амплітудне) значення сили струму; ω –циклічна (або кругова) частота, яка зв’язана з періодом коливань Т, або частотою коливань ν співвідношенням (54.2); j_о – початкова фаза коливань.

w=2p/T=2pv (54.2)

Якщо визначити енергоздатність змінного струму, то можна встановити величину, яка отримала назву ефективного (або діючого) значення сили струму, а саме:

ефективне значення сили змінного струму І_еф – сила такого постійного струму, який за своєю енергоздатністю (наприклад, виділення теплоти за той же час) еквівалентний даному змінному струму.

Для синусоїдальних струмів їх ефективне значення І_еф менше максимального І_mах в 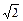разів (формула (54.3)). Аналогічний вираз маємо для ефективного значення напруги змінного струму (формула (54.4)).

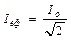(54.3)

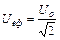(54.4)

2. АКТИВНИЙ ОПІР В КОЛІ ЗМІННОГО СТРУМУ

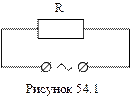Активний опір - та частина опору електричного кола змінного струму, на якій відбувається виділення джоулевого тепла Q (54.5).

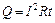(54.5)

Для характеристики кіл змінного струму зручно користуватись методом векторних діаграм, де максимальні значення сили струму I_o і напруги U_o зображаються відповідними векторами. Так, на активному опорі коливання сили струму і напруги відбуваються в однаковій фазі, тому векторна діаграма змінного струму з активним опором буде мати вигляд, зображений на рис. 54.2.

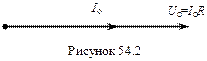При малих частотах струму активний опір кола наближається до його опору при постійному струмі. При високих частотах виникають особливі ефекти, які приводять до збільшення опору кола з активним опором R. В цьому колі коливання змінного струму І співпадають по фазі з коливаннями напруги U. При високих частотах струму можливий поверхневий ефект, коли струм у провіднику тече тільки по його поверхні. Крім того, відбуваються втрати на перемагнічування провідника.

3. ЄМНІСТЬ У КОЛІ ЗМІННОГО СТРУМУ

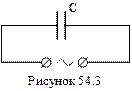Конденсатор являє собою систему двох провідників, які розділені діелектриком. Наприклад, плоский конденсатор – дві близько розташовані паралельні пластини (обкладинки). Ємність конденсатора, фізична величина, рівна відношенню заряду на пластинах q до різниці потенціалів j₁-j₂=U між ними.

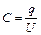, (54.6)

Для кола постійного струму конденсатор є розривом такого кола, струм відсутній, так як між обкладинками конденсатора відсутні вільні заряди (знаходиться вакуум або діелектрик). Якщо ж конденсатор С ввімкнути в коло змінного струму (рис.54.3), то його обкладинки будуть перезаряджатись і в колі виникне електричний струм. Але коливання струму не співпадають за фазою з коливаннями напруги. Дійсно, якщо напруга на обкладинках конденсатора збільшується від нуля до максимального значення, то саме на початку цього збільшення почнеться найбільш інтенсивна зарядка конденсатора. Коли ж напруга досягне максимального значення, зарядка конденсатора припиниться і струм стане рівним нулю.

Кількісні співвідношення між коливаннями сили струму і напруги в колі змінного струму з конденсатором встановлюються наступним чином.

Зміна заряду конденсатора на dq призводить до зміни напруги між обкладинками на dU, так, що

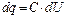, (54.7)

тоді миттєве значення сили струму i буде дорівнювати

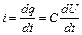. (54.8)

Якщо напруга між обкладинками конденсатора змінюється за законом

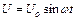, (54.9)

де U_o – максимальне значення напруги, то згідно 54.8 (взявши похідну), отримаємо

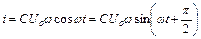. (54.10)

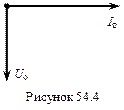Таким чином, коливання сили струму в колі змінного струму з конденсатором випереджають коливання напруги за фазою на p/2 і векторна діаграма такого кола матиме наступний вигляд (рис. 54.4).

Максимальне значення сили струму в колі змінного струму з конденсатором, як випливає з (54.10) буде дорівнювати

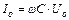. (54.11)

Якщо порівняти це значення із законом Ома 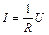, то легко помітити, що роль опору в колі змінного струму з ємністю грає величина

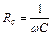, (54.12)

яка називається реактивним ємнісним опором (реактивний – від латинського слова – протидія).

4. ІНДУКТИВНІСТЬ У КОЛІ ЗМІННОГО СТРУМУ

Якщо в провідному контурі тече струм силою І, то такий струм створює магнітне поле і площу контуру пронизує магнітний потік Ф, який пропорційний силі струму в цьому контурі

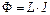, (54.13)

де коефіцієнтом пропорційності є величина L, яка називається індуктивністю і вимірюється в Гн (генрі[1]), так, що 1 Гн = 1 Вб/А.

При зміні струму на dI магнітний потік змінюється на dФ

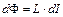, (54.14)

тоді згідно закону електромагнітної індукції

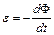, (54.15)

в цьому контурі виникає ЕРС, яка отримала назву ЕРС самоіндукції

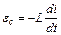. (54.16)

З (54.16) випливає, що 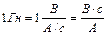, тобто 1 Гн індуктивність такого контуру в якому при зміні сили струму з швидкістю 1 А/с виникає ЕРС самоіндукції 1 В.

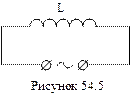Якщо в колі змінного струму знаходиться індуктивність L, наприклад, соленоїд (рис.54.5), то внаслідок явища самоіндукції коливання сили струму не будуть співпадати по фазі з коливаннями напруги. Дійсно, збільшенню струму в соленоїді перешкоджає ЕРС самоіндукції, внаслідок чого сила струму досягає максимального значення пізніше в порівнянні з максимальним значенням напруги.

Таким чином струм в колі з індуктивністю зумовлений дією прикладеної змінної напруги U та ЕРС самоіндукції e і закон Ома для такого кола прийме вигляд:

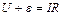. (54.17)

Розглянемо коло, де активний опір відсутній (R=0), тоді

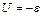, (54.18)

враховуючи (54.16) отримаємо

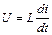. (54.19)

Нехай струм в колі змінюється за законом

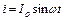, (54.20)

Взявши похідну згідно (54.14) будемо мати

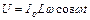, (54.21)

і порівнюючи з (54.20) бачимо, що коливання сили струму відстають за фазою на p/2, що можна зобразити векторною діаграмою

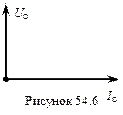В (54.21) величина 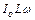визначає максимальне (амплітудне) значення напруги

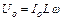. (54.22)

Порівнюючи цей вираз із законом Ома U=IR легко бачити, що величина Lw грає роль опору, який називається індуктивним реактивним опором

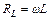. (54.23)

5. АКТИВНИЙ ОПІР, ІНДУКТИВНІСТЬ ТА ЄМНІСТЬ У КОЛІ ЗМІННОГО СТРУМУ

В електричних колах можуть бути одночасно активні та реактивні опори. На рис.54.7 наведена схема послідовного з’єднання активного опору R, індуктивності L та ємності (конденсатора) С.

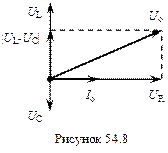
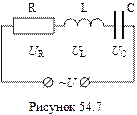Враховуючи фазові співвідношення між коливаннями сили струму і напруги на кожному елементі такого кола, векторна діаграма кола буде мати вигляд (54.8), де U_R – максимальна напруга на активному опорі, U_L – на індуктивності, U_C – на ємності, I_o – максимальне значення струму, однакове для всіх ділянок. Виконавши векторне додавання напруг, будемо мати, що модуль результуючої напруги дорівнює

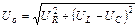, (54.24)

враховуючи (54.11) та (54.22) одержимо

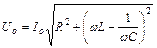, (54.25)

або

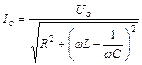, (54.26)

Отриманий вираз називають законом Ома для кола змінного струму, а величину

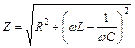, (54.27)

називають повним опором, або імпедансом (від грецького – „повний”).

6. ПРИНЦИП ЕКСПЕРИМЕНТАЛЬНОГО ВИЗНАЧЕННЯ ЄМНОСТІ КОНДЕНСАТОРА МЕТОДОМ ВИМІРЮВАННЯ ЙОГО РЕАКТИВНОГО ОПОРУ.

Якщо в колі змінного струму знаходиться тільки ємнісний опір (конденсатор), то з (54.26) отримаємо (54.28). Виміривши ефективні значення напруги та струму в колі, яке містить конденсатор, за формулою (54.28) можна підрахувати ємнісний опір конденсатора, а виміривши частоту змінного струму ν і враховуючи, що ω=2πν, отримаємо вираз (54.29) для розрахунку ємності конденсатора.

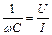(54.28)

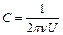(54.29)

Таким чином, принцип даного експериментального методу визначення ємності конденсатора базується на вимірюванні його реактивного опору в колі змінного струму.

7. ВИЗНАЧЕННЯ ІНДУКТИВНОСТІ СОЛЕНОЇДА

Ідею вимірювання реактивних опорів використовують для визначення індуктивності різноманітних соленоїдів, обмоток, контурів і т.п.

Так, якщо в колі змінного струму маємо котушку індуктивності, активний опір обмотки якої становить R, то закон Ома для повного кола матиме вигляд (54.30), звідки отримаємо формули (54.31) та (54.32) для розрахунку шуканої індуктивності L.

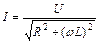(54.30)

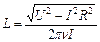(54.31)

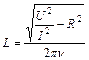(54.32)

На основі даного експериментального методу можна визначити магнітну проникність речовини[2] μ, яка знаходиться в соленоїді (магнітна проникність осердя). Дійсно, індуктивність соленоїда L визначається співвідношенням (54.33),

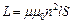, (54.33)

де μ₀ – магнітна стала, яка дорівнює 4π×10^-7 Гн/м; n – кількість витків на одиницю довжини соленоїда; S – площа його поперечного перерізу; μ – магнітна проникність середовища (в даному випадку – магнітна проникність осердя, яке знаходиться в соленоїді). Вимірявши індуктивність L₀ соленоїда у відсутності осердя (μ = 1, як для повітря), а потім – індуктивність цього соленоїда L з осердям, визначимо магнітну проникність матеріалу цього осердя за формулою (54.34). (Ця формула випливає з порівняння співвідношень L = μμ₀n²ІS та L₀ = μ₀n²IS.)

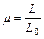(54.34)

8. ПОХИБКИ МЕТОДУ

Згідно з робочими формулами (54.29), (54.31), (54.32) визначення ємності конденсатора та індуктивності соленоїда вимагає вимірювання ефективних значень сил струмів та напруг, а також частоти ν струму. Вплив похибки кожного вимірювання на кінцевий результат можна оцінити з формули похибок. Нагадаємо, що для цього: 1) робочу формулу логарифмують при натуральній основі; 2) отриманий вираз диференціюють; 3) заміняють знаки диференціала “d” на знак абсолютної похибки вимірювання “Δ” і враховують правило складання похибок. Провівши такі математичні операції, будемо мати формулу (54.35) для відносної похибки ємності, а для індуктивності – формулу (54.36).

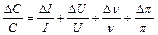(54.35)

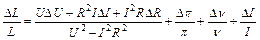(54.36)

Абсолютні похибки сили струму та напруги можна визначити через класи точності відповідних електровимірювальних приладів. У даній роботі джерелом змінного струму є електромережа промислової частоти ν = 50 Гц, де Δν = ± 0,5 Гц. Що стосується похибки числа π, то взявши π = 3,14 ,Δπ = ±0,005. Виконання роботи не вимагає окремого вимірювання активного опору обмотки соленоїда. На лабораторному стенді вказані величини R та ΔR.