Вимірювання еластичності. Лінійно-логарифмічна модель

Розглянемо експоненціальну регресійну модель

,

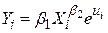(4.4.1)

яка після логарифмування обох частин може бути подана у вигляді

.

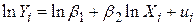(4.4.2)

Якщо ми запишемо (4.4.2) у вигляді

,

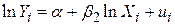(4.4.3)

де 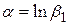, то побачимо, що ця модель лінійна за параметрами 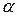і , а також за логарифмами змінних Х і Y. Отже, для знаходження 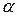і може бути застосований МНК. Така модель ще називається “подвійною логарифмічною” або “логарифмічною лінійною”.

Якщо припущення класичної лінійної регресійної моделі виконуються, то параметри (4.4.3) можуть бути оцінені за МНК із рівняння

,

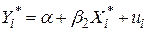(4.4.4)

де 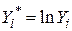, 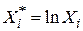. Отримані за МНК оцінки 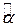і 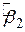будуть найкращими незміщеними лінійними оцінками для 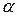і , відповідно.

Перевагою цієї моделі є те, що кутовий коефіцієнт є мірою еластичності Y по відношенню до Х, тобто визначає відсоток зміни Y для даного (малого) відсотка зміни Х. Так, якщо Y зображує попит на товар, а Х – ціну одиниці товару, то вимірює величину еластичності попиту за ціною, параметр lnY, що становить в економіці значний інтерес.

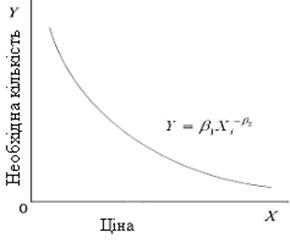
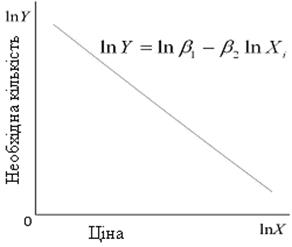
Рис. 4.2 . Експоненціальна модель Рис. 4.3. Лінійно-логарифмічна модель

Якщо співвідношення між величиною попиту і ціною таке, як зображено на рис. 4.2, то подвійне логарифмічне перетворення даватиме оцінку еластичності ціни ( ).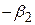

Слід зазначити два особливі моменти лінійної логарифмічної моделі: ця модель припускає, що коефіцієнт еластичності між Y і Х ( ) залишається постійним на всьому проміжку зміни Х. Цю властивість можна перевірити, оскільки еластичність Y по Х обчислюється за формулою

.

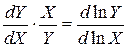Якщо підставити в неї 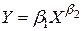, то отримаємо

.

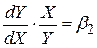Ця властивість пояснює, чому дана модель називається моделлю з постійною еластичністю. Іншими словами, зміна lnY при одиничній зміні lnХ, тобто еластичність , залишається незмінною незалежно від точки lnX, в якій проводиться вимірювання (рис.4.3). Іншою особливістю моделі є те, що, хоча 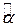і 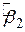є незміщеними оцінками 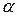і , 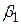(параметр, що входить у початкову модель 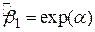) є зміщеною оцінкою. У більшості практичних задач, проте, цей член має другорядне значення і немає необхідності в отриманні незміщеної оцінки.