Продукт (GNP) у цінах 1972 р. у доларах США, 1974–1983 рр.
| Рік | GPDI, млрд дол | GPDI, млн дол | GNP, млрд. дол | GNP, млн. дол |
| 195,5 | 1246,3 | |||
| 154,8 | 1231,6 | |||
| 184,5 | 1298,2 | |||
| 214,2 | 1369,7 | |||
| 236,7 | 1438,6 | |||
| 236,3 | 1479,4 | |||
| 208,5 | 1475,0 | |||
| 230,9 | 1512,2 | |||
| 194,3 | 1480,0 | |||
| 221,0 | 1534,7 |
Припустимо, що в регресії GPDI за GNP один дослідник використовує дані, що обчислюються в мільярдах, а інший – у мільйонах доларів. Чи будуть результати регресійного аналізу однаковими в обох випадках? Якщо ні, то який результат слід використовувати? Інакше, чи впливають одиниці, в яких вимірюються Y і Х, на результати регресійного аналізу?
Щоб відповісти на це запитання, зробимо так. Хай
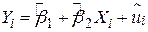 , ,
| (4.2.1) |
де 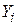 – GPDI,
– GPDI, 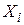 – GNP.
– GNP.
Визначимо
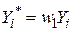 , ,
| (4.2.2) |
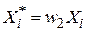 , ,
| (4.2.3) |
де 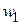 і
і 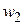 – константи, що називаються масштабними чинниками.
– константи, що називаються масштабними чинниками. 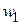 і
і 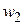 можуть збігатися, а можуть бути різними.
можуть збігатися, а можуть бути різними.
З рівнянь (4.2.2) і (4.2.3) зрозуміло, що 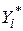 і
і 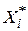 змінюють шкалу вимірювань
змінюють шкалу вимірювань 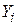 і
і 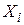 . Так, якщо
. Так, якщо 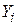 і
і 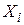 вимірюються в мільярдах доларів, а ми хочемо перейти до вимірювання в мільйонах доларів, то
вимірюються в мільярдах доларів, а ми хочемо перейти до вимірювання в мільйонах доларів, то
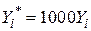 , ,
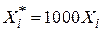 . .
|
У цьому випадку 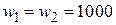 .
.
Тепер розглянемо регресію, застосовуючи змінні 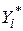 і
і 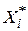 :
:
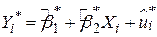 , ,
| (4.2.4) |
де 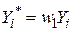 ,
, 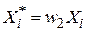 і
і 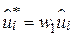 .
.
Ми можемо отримати зв’язок між парами:
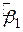 і і 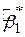 , ,
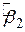 і і 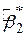 , ,
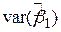 і і 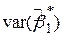 , ,
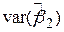 і і 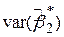 , ,
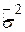 і і 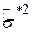 , ,
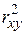 і і 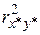 . .
|
За методом найменших квадратів ми маємо
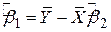 , ,
| (4.2.5) |
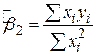 , ,
| (4.2.6) |
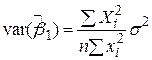 , ,
| (4.2.7) |
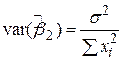 , ,
| (4.2.8) |
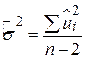 . .
| (4.2.9) |
Застосовуючи МНК до (6.2.4), одержуємо
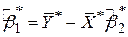 , ,
| (4.2.10) |
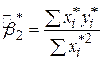 , ,
| (4.2.11) |
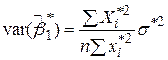 , ,
| (4.2.12) |
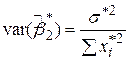 , ,
| (4.2.13) |
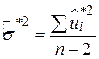 . .
| (4.2.14) |
З цієї рівності легко отримати співвідношення між двома наборами оцінок параметрів. Усе, що для цього потрібно, так це застосувати рівності: 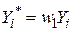 (або
(або 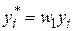 );
); 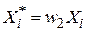 (або
(або 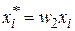 );
); 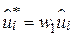 ;
; 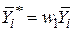 ;
; 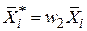 . Застосовуючи ці співвідношення, нескладно отримати рівності, що цікавлять нас:
. Застосовуючи ці співвідношення, нескладно отримати рівності, що цікавлять нас:
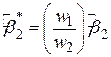 , ,
| (4.2.15) |
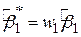 , ,
| (4.2.16) |
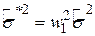 , ,
| (4.2.17) |
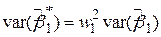 , ,
| (4.2.18) |
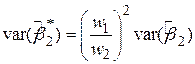 , ,
| (4.2.19) |
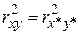 . .
| (4.2.20) |
Із цих формул зрозуміло, як за наслідками регресійного аналізу в одних одиницях вимірювання перейти до інших одиниць вимірювання при заданих значеннях масштабного чинника.
Дата добавления: 2016-07-27; просмотров: 1617;











