Вибіркова регресійна функція (SRF)
Обмежуючи наше обговорення випадком дослідження популяції Y, відповідної деякому фіксованому X, ми навмисно уникали розгляду вибіркових даних. Уміщені в табл. 1.1 дані стосуються всієї популяції. Проте настав час звернутися до розгляду вибіркових даних, оскільки на практиці такі випадки зустрічаються найчастіше. Отже, нашою задачею є обчислення PRF на основі вибіркової, тобто неповної інформації.
Наприклад, нам була відома не вся інформація з табл. 1.1, а лише її частина, отримана шляхом випадкової вибірки з цієї таблиці. Отримана таким чином інформація подана в табл. 1.3.
Таблиця 1.3
| Х | ||||||||||
| Y |
На відміну від табл. 1.1, ми зараз маємо єдине значення Y, відповідне фіксованому значенню X; кожне Y (при фіксованому X) з табл. 1.4 вибране випадковим чином із табл. 1.1.
Питання полягає в такому: чи можемо ми за вибірковими даними табл. 1.1 розрахувати середні тижневі споживацькі витрати за всією популяцією? Іншими словами, чи можемо обчислити PRF за вибірковими даними? Інтуїтивно зрозуміло, що ми не можемо обчислити PRF «точно» через флуктуації за вибіркою. Щоб побачити це більш наочно, припустимо, що ми маємо іншу випадкову вибірку з табл. 1.1, наведену в табл. 1.4.
Таблиця 1.4
| Х | ||||||||||
| Y |
Дані з таблиць 1.4 і 1.5 зобразимо на графіку (рис. 1.3). На рис. 1.3 дві прямі вибіркової регресії проведені так, щоб найкращим чином відповідати даним таблиць: SRF1 ґрунтується на даних першої вибірки, а SRF2 – другої. Яка з цих двох ліній є істинна лінія регресії популяції? Якщо не брати до уваги рис. 1.1, де зображена лінія регресії популяції, то не існує способу, що дозволяє напевно стверджувати, яка з ліній являє собою істинну лінію регресії популяції. Показанні на рис. 1.3 лінії називаються лініями вибіркової регресії (sample regression lines). Передбачається, що вони зображають лінію регресії популяції, проте через флуктуації за вибіркою вони в кращому разі зображають апроксимацію. У загальному випадку для N вибіркових даних може бути отриманий N SRF і, швидше за все, усі вони будуть різними.
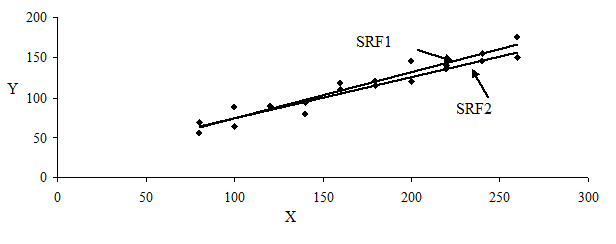
Рис. 1.3. Лінії вибіркової регресії SRF1, SRF2
Тепер за аналогією з поняттям функції регресії популяції PRF можна ввести поняття функції вибіркової регресії SRF. Аналог формули (1.2.2) може бути записаний у вигляді
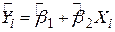 , ,
| (1.6.1) |
де 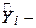 математичне сподівання E(Y½
математичне сподівання E(Y½  ), обчислене на основі вибіркових даних;
), обчислене на основі вибіркових даних; 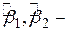 коефіцієнти регресії, обчислені на основі вибіркових даних.
коефіцієнти регресії, обчислені на основі вибіркових даних.
Тепер за аналогією з уявленням PRF у двох еквівалентних формах (1.2.2) і (1.4.2) ми можемо подати SRF (1.6.1) у стохастичному вигляді
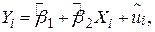
| (1.6.2) |
де 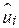 - залишковий член, отриманий за вибірковими даними.
- залишковий член, отриманий за вибірковими даними.
Підсумовуючи сказане, ми уявляємо собі основну задачу регресійного аналізу в обчисленні PRF
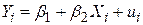
|
на основі SRF
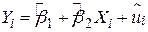 . .
|
Частіше на практиці доводиться проводити аналіз на основі вибіркових даних, а не даних за всією популяцією. Але, зважаючи на флуктуації вибіркових даних, отримана на підставі SRF функція PRF є в кращому разі апроксимацією істинної PRF.
Для X =  ми маємо одне спостереження Y =
ми маємо одне спостереження Y = 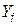 . По відношенню до SRF
. По відношенню до SRF 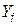 може бути подано таким чином:
може бути подано таким чином:
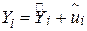 , ,
| (1.6.3) |
а по відношенню до PRF його можна подати у вигляді
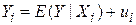 . .
| (1.6.4) |
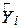 дає в порівнянні з істинним значенням
дає в порівнянні з істинним значенням 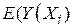 для
для  завищене значення. Зрозуміло, що подібні заниження і завищення пояснюються флуктуаціями вибіркових даних.
завищене значення. Зрозуміло, що подібні заниження і завищення пояснюються флуктуаціями вибіркових даних.
Основне питання полягає в такому: розуміючи, що SRF є не більше ніж апроксимація PRF, чи можемо ми запропонувати правило або метод, що дозволяли б якомога більше наблизитися до PRF? Іншими словами, яким чином побудувати SRF так, щоб 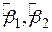 були б якомога ближчі до
були б якомога ближчі до 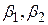 , хоча ми й не знаємо істинні значення
, хоча ми й не знаємо істинні значення 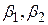 . Відповідь на це питання така: ми запропонуємо метод, що дозволить сконструювати SRF так, щоб вона найбільш точно відображала властивості PRF. Надзвичайно цікавим є той факт, що ми зможемо це зробити навіть не маючи нагоди визначити дійсну PRF.
. Відповідь на це питання така: ми запропонуємо метод, що дозволить сконструювати SRF так, щоб вона найбільш точно відображала властивості PRF. Надзвичайно цікавим є той факт, що ми зможемо це зробити навіть не маючи нагоди визначити дійсну PRF.
Дата добавления: 2016-07-27; просмотров: 2148;











