Важливість урахування складової стохастичного збурення

Як було зазначено в попередньому розділі, випадкова складова 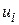враховує колективний вплив на Y всіх змінних, які не включені в модель. Очевидно постає питання, чому б не ввести в модель ці змінні, або інакше, чому б не доповнити множинну регресійну модель можливою великою кількістю змінних? Причин існує багато.

1. Неясність теорії. Теорія (якщо вона взагалі існує), що визначає характер Y, може бути (що частіше всього й трапляється) неповною. Ми можемо знати напевно, що тижневий дохід X сім’ї впливає на її споживацькі витрати Y, проте ми можемо не знати або не бути впевненими у впливі на Y інших змінних. Отже, 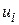може бути застосований як заміна для всіх виключених або опущених у моделі змінних.

2. Неповнота даних. Навіть якщо нам і відомо, що собою являють деякі змінні, виключені з моделі, і отже, має місце множинна, а не найпростіша регресія, нам може бути недоступна кількісна інформація щодо цих змінних. В емпіричних дослідженнях дуже часто трапляється так, що дані, необхідні нам, виявляються недоступними. Наприклад, ми могли б ввести в модель на додачу до доходу як пояснювальну змінну накопичені заощадження сім’ї. Але, на жаль, інформація про грошові заощадження сім’ї виявляється недоступною. Отже, ми вимушені виключити цю змінну з моделі всупереч тому, що вона значною мірою впливає на пояснення споживацьких витрат сім’ї.

3. Протиставлення головних змінних периферійним змінним. Припустимо, що в нашій моделі “споживання - дохід” окрім доходу X₁ враховуються кількість дітей в сім’ї X₂, стать X₃, віросповідання X₄, рівень освіти X_5, регіон мешкання X₆, які також впливають на рівень споживацьких витрат. Але цілком можливо, що сумарний вплив усіх або деяких із цих змінних може бути таким незначним, що з погляду на їх внесок, і зважаючи на ускладнення моделі, їх не слід включати у модель в явному вигляді. Можна сподіватися, що їх сумарний вплив враховується як випадкова величина .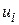

4. Властива природі людини випадковість. Навіть за умови введення в модель усіх змінних, все одно залишається властива індивідуальному значенню Y випадковість, яку, як би ми не хотіли, пояснити неможливо. Стохастична складова u може дуже добре відображати цю властиву випадковість.

5. Слабка довіра до змінних. Хоча класична регресійна модель припускає точне вимірювання змінних Y і X, на практиці дані можуть містити помилки. Розглянемо, наприклад, добре відому модель функції споживання Мільтона Фрідмана (Milton Friedman). Згідно з нею постійне споживання (Yр) вважається функцією постійного доходу (Xр). Але оскільки дані за цими змінними не є доступними безпосередньо, на практиці ми застосовуємо змінні, що їх замінюють, такі як поточне споживання (Y) і поточний дохід (X), за якими дані доступні. Оскільки дані, доступні за Y і X, не обов’язково повинні збігатися з даними за змінними Yр і Xр, то існує проблема похибки вимірювання. Збурююча складова u може при цьому являти собою помилку вимірювання. Як ми побачимо далі, наявність похибки вимірювання серйозно позначається на точності визначення коефіцієнтів b.

6. Дотримання принципу найбільшої простоти. Згідно з відомою тезою про те, що модель потрібно зберігати в найпростішому вигляді, поки не доведена її неадекватність, є природним бажання зберегти регресійну модель у найпростішому вигляді. Якщо ми можемо пояснити характер Y достатньо докладно за допомогою двох або трьох пояснювальних змінних і якщо наша теорія не припускає, що інші змінні повинні бути включені в модель, навіщо їх тоді вводити? Нехай u_i замінює собою всю решту змінних. Звичайно ж, не слід виключати з моделі змінні, що стосуються справи, лише заради збереження простоти моделі.

7. Неправильний вид функціональної залежності. Навіть якщо ми маємо теоретично коректні пояснювальні змінні, що описують явище, а також маємо достовірні дані, що стосуються цих змінних, дуже часто ми не знаємо вигляду функціональної залежності між регресандом і регресорами. Функція споживацьких витрат є лінійною по відношенню до доходу чи нелінійною? У двовимірному регресійному аналізі уявлення про вигляд функціональної залежності може бути отримане з графіка. У множинному регресійному аналізі досить нелегко визначити правильний вигляд функціональної залежності, оскільки неможливо візуально скласти уявлення про неї.

З усіх цих причин, що стосуються стохастичного збурення, складова 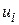відіграє в регресійному аналізі надзвичайно важливу роль.