Метод найменших квадратів

Метод найменших квадратів (МНК) був запропонований Карлом Фрідріхом Гауссом – німецьким математиком. При деяких припущеннях МНК має дуже привабливі статистичні властивості, які роблять його одним із щонайпотужніших і популярних методів регресійного аналізу. Для того щоб зрозуміти цей метод, слід спочатку пояснити принцип найменших квадратів.

Пригадаємо двовимірну PRF:

.

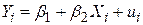Як нами було відзначене раніше, PRF не є об'єктом, який можна отримати прямо. Ми оцінюємо його з вибіркової регресійної функції (SRF):

,

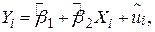
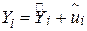де 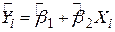- оцінена величина .

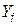Для визначення SRF зобразимо спочатку (1.6.3) у вигляді

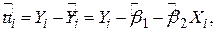
(2.1.1)

який підказує, що 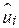(залишки, стохастична або випадкова складова) є різницею між дійсною та оціненою величиною Y.

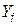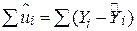Тепер для даних N пар спостережень над ( , ), визначимо SRF так, щоб вона була розташована якомога ближче до дійсних Y. Для цього можна обрати такий критерій: виберемо SRF так, щоб сума залишків була наскільки можливо мала. Хочаінтуїтивно такий критерій здається привабливим, насправді він не дуже вдалий, як це можна бачити з гіпотетичного прикладу, показаного на рис. 2.1.

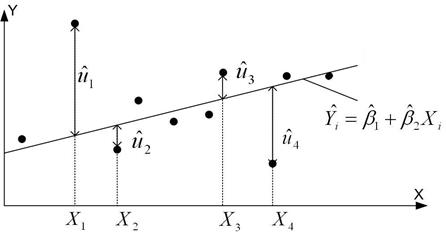
Рис. 2.1. Критерій найменших квадратів

Якщо ми візьмемо критерій мінімізації 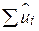, то згідно з рисунком залишки 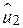і 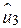мають у сумі 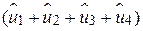те ж значення, що й 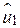і 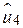, хоча перші два залишки набагато ближчі до SRF, ніж два останніх. Іншими словами, усі залишки мають однакові значення безвідносно до того, наскільки вони близько або далеко розташовані від SRF. Щоб переконатися в цьому, хай 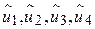на рис. 2.1 набувають, відповідно, значень 10, –2, 2, –10. Сума цих залишків є нуль, хоча 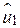і 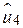розташовані набагато далі, ніж 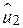і 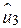. Ми можемо уникнути подібної ситуації, якщо візьмемо критерій найменших квадратів, який стверджує, що SRF можна фіксувати, якщо

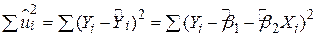
(2.1.2)

набуває найменшого значення. За рахунок піднесення у квадрат цей метод надає більшого значення таким залишкам як 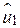і 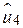порівняно з 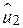і 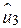. Як було відзначено раніше, при критерії мінімуму 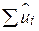можлива ситуація, коли сума залишків мала, але 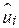широко розкидані навколо лінії SRF. Проте це неможливо при виборі критерію мінімуму суми квадратів залишків, оскільки чим більше 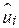(за абсолютною величиною), тим більше 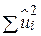. Наступне обґрунтовування переваги МНК над іншим критерієм полягає в тому, що отримані за МНК оцінки мають деякі привабливі з погляду статистики властивості.

З (2.1.2) очевидно, що

,

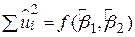(2.1.3)

тобто сума квадратів залишків є функція від оцінок 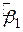і 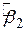. Для будь-якої заданої сукупності даних вибір різних величин для 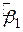і 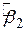дає різні залишки 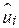і, отже, різну величину 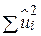. Щоб було зрозуміліше, розглянемо гіпотетичні дані Y і X, наведені в перших двох колонках табл. 2.1.

Таблиця 2.1