Распределение Пуассона.

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, непоявления q = 1 – p.

Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины X.

Если число испытаний велико, а вероятность появления события 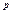в каждом испытании мала, то вероятность того, что некоторое событие появиться k раз в 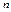испытаниях, приближенно вычисляется по формуле:

,

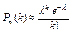где 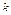– число появлений событий в 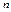независимых испытаниях,

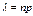– среднее число появлений событий в 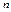испытаниях.

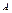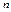Случайная величина, характеризующая число наступлений события в независимых испытаниях, распределена по закону Пуассона, если

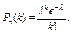
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона:

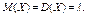
Замечание. Имеются специальные таблицы, пользуясь которыми можно найти 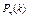, зная k и 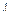(Приложение 2).

Пример 5.2. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Решение.

По условию, п = 5000, р = 0,0002, k = 3.

Найдем :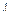

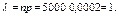
По формуле Пуассона искомая вероятность приближенно равна: