Основные виды выборок
При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторнойназывают выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности, эго требование коротко формулируют так: выборка должна быть репрезентативной (представительной).
Выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.
Способы отбора
На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида:
1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся:
а) простой случайный бесповторный отбор (объекты извлекают по одному из всей генеральной совокупности);
б) простой случайный повторный отбор.
2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся:
а) типический отбор (объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Например, если детали изготовляют на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности.);
б) механический отбор (генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20% изготовленных станком деталей, то отбирают каждую пятую деталь; если требуется отобрать 5% деталей, то отбирают каждую двадцатую деталь, и т. д.);
в) серийный отбор (объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Например, если изделия изготовляются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.
Вариационный ряд
Основная форма представления выборочной совокупности – вариационные ряды.
Пусть посредством независимых испытаний, проведенных в одинаковых условиях, получены числовые значения х1, х2, . . ., хп. Располагают эти значения в порядке возрастания 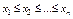 и называют полученную последовательность вариационным рядом, а сами значения
и называют полученную последовательность вариационным рядом, а сами значения 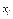 – вариантами.
– вариантами.
Число, показывающее, сколько раз встречается в выборке вариант 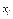 , называют частотой варианта и обозначают
, называют частотой варианта и обозначают 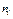 , причем
, причем 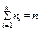 (k – количество различных вариант).
(k – количество различных вариант).
Отношение числа вариантов к объему выборки (или общему числу наблюдений) 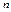 называют относительной частотой наблюдения.
называют относительной частотой наблюдения.

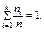
Вариационный ряд показывает, каким образом варианты связаны с их частотами в выборке.
Вариационные ряды бывают двух типов: интервальные и безынтервальными.
В интервальном вариационном ряду частоты характеризующие повторяемость вариант в выборке, распределяются по интервалам группировки. Интервальный вариационный ряд строится, если изучаемый признак варьирует непрерывно, но используется и для дискретно варьирующих признаков в тех случаях, когда признак варьирует в широких пределах.
Пример 7.3.
| Превышение разрешенной скорости движения (км/ч) | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | больше 60 |
| Количество нарушений |
В безынтервальном вариационном ряду частоты распределяются непосредственно по значениям варьирующего признака. Для построения безынтервального вариационного ряда необходимо варианты выборки расположить в порядке возрастания или убывания (проранжировать) и затем подсчитать, сколько раз каждая из них встречается в выборке. Безынтервальный вариационный ряд применяется в тех случаях, когда исследуемый признак варьирует дискретно и слабо.
Пример 7.4.
| Экзаменационная оценка | ||||||||||
| Количество учащихся |
Дата добавления: 2016-07-27; просмотров: 2978;











