Математическое ожидание случайной величины
Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины.
К числу важных числовых характеристик относится математическое ожидание.
Математическое ожидание приближенно равно среднему значению случайной величины.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Если случайная величина характеризуется конечным рядом распределения:
| Х | х1 | х2 | х3 | … | хп |
| Р | р1 | р2 | р3 | … | рп |
то математическое ожидание М(Х) определяется по формуле:
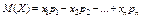
или
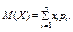
Математическое ожидание непрерывной случайной величины определяется равенством:
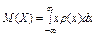 ,
,
где 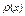 – плотность вероятности случайной величины Х.
– плотность вероятности случайной величины Х.
Пример 4.7. Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.
Решение:
Случайная величина Х принимает значения 1, 2, 3, 4, 5, 6. Составим закон ее распределения:
| Х | ||||||
| Р | 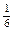
| 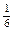
| 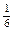
| 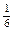
| 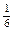
| 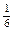
|
Тогда математическое ожидание равно:
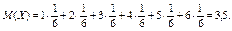
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной:
М (С) = С.
2. Постоянный множитель можно выносить за знак математического ожидания:
М (СХ) = СМ (X).
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M(XY) = M(X)M(Y).
Пример 4.8. Независимые случайные величины X и Y заданы следующими законами распределения:
| Х | Y | ||||||
| Р | 0,6 | 0,1 | 0,3 | Р | 0,8 | 0,2 |
Найти математическое ожидание случайной величины XY.
Решение.
Найдем математические ожидания каждой из данных величин:
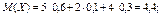
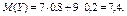
Случайные величины X и Y независимые, поэтому искомое математическое ожидание:
M(XY) = M(X)M(Y)= 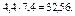
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
М (X + Y) = М (X) + М (Y).
Следствие.Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
Пример 4.9. Производится 3 выстрела с вероятностями попадания в цель, равными р1 = 0,4; p2 = 0,3 и р3 = 0,6. Найти математическое ожидание общего числа попаданий.
Решение.
Число попаданий при первом выстреле есть случайная величина Х1, которая может принимать только два значения: 1 (попадание) с вероятностью р1 = 0,4 и 0 (промах) с вероятностью q1 = 1 – 0,4 = 0,6.
Математическое ожидание числа попаданий при первом выстреле равно вероятности попадания:

Аналогично найдем математические ожидания числа попаданий при втором и третьем выстрелах:
М(Х2) = 0,3 и М(Х3)=0,6.
Общее число попаданий есть также случайная величина, состоящая из суммы попаданий в каждом из трех выстрелов:
Х = Х1 + Х2 + Х3.
Искомое математическое ожидание Х находим по теореме о математическом, ожидании суммы:
М(X) = M(Xl + X2 + X3) = M(X1) + M(X2) + M (X3) = 0,4 + 0,3 + 0,6 = 1,3 (попаданий).
Дата добавления: 2016-07-27; просмотров: 5645;











