Биноминальное распределение

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, непоявления q = 1 – p.

Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, ..., либо п раз. Таким образом, возможные значения X таковы: х₁= 0, x₂ = 1, x₃ = 2, . . ., x_n+1= n. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

,

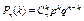где k = 0, 1, 2, .... п.

Данная формула и является аналитическим выражением искомого закона распределения.

Биноминальнымназывают закон распределения дискретной случайной величины 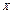- числа появлений событий в 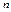независимых испытаниях, в каждом из которых вероятность появления события равна 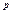; вероятность возможного значения 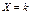(числа 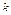появлений события) вычисляют по формуле Бернулли:

,

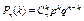где .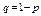

Таким образом, первый член разложения р^п определяет вероятность наступления рассматриваемого события п раз в п независимых испытаниях; второй член 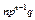определяет вероятность наступления события п – 1 раз; ...; последний член q^п определяет вероятность того, что событие не появится ни разу.

Напишем биномиальный закон в виде таблицы:

Х	п	п-1	…	k	…	0
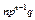
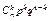
Р	рп		…		…	qп

При этом математическое ожидание и дисперсия соответственно равны:

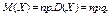
Пример5.1. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X — числа выпадений «герба».

Решение.

Вероятность появления «герба» в каждом бросании монеты 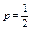, следовательно, вероятность непоявления «герба»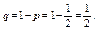

При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: x₁ = 2, х₂ = 1, х₃ = 0. Найдем вероятности этих возможных значений по формуле Бернулли:

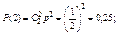
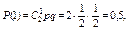
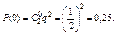
Напишем искомый закон распределения:

Контроль: 0,25 + 0,5 + 0,25 = 1.