Дисперсия случайной величины. Среднее квадратическое отклонение

Мы рассмотрели число, которое характеризует поведение случайной величины в среднем. Но среднее значение далеко не всегда дает даже общее представление о поведении случайной величины.

Есть еще одна характеристика, которая зачастую несет не менее важную информацию, — это разброс (или рассеивание) случайной величины вокруг ее среднего значения. Вспомним известную шутку о том, что средняя температура по больнице, 36,6°. Ведь это вполне может быть так, если часть больных имеет повышенную температуру, а часть пониженную. Тогда чем же будет отличаться поведение случайной величины, равной температуре больного человека, от поведения величины, равной температуре здорового? И та, и другая величины подвержены колебаниям вокруг некоторого среднего значения (возможно, даже одинакового), но очевидно, что у больных величина этих колебаний будет больше. Попробуем выяснить, какое выражение может претендовать на роль средней меры рассеивания случайной величины вокруг ее среднего значения.

Дисперсиейслучайной величины называется математическое ожиданиеквадрата ее отклонения:

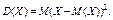
Дисперсия дискретной случайной величины вычисляется по формуле:

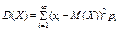
или

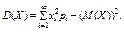
Средним квадратическим отклонением(стандартом) случайной величины называется арифметический корень из дисперсии, т.е.

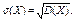
Пример 4.10. Найти дисперсию числа очков, выпадающих при бросании игральной кости.

Решение:

Закон распределения случайной величины Х и ее математическое ожидание М(Х) = 3,5 были приведены в примере 4.7.

Вычислим дисперсию:

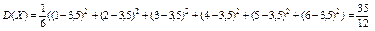
Дисперсия непрерывной случайной величины определяется равенством:

.

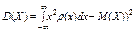Свойства дисперсии:

1.Дисперсия постоянной величины С равна нулю:

D (С) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

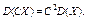
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

D (X + Y) = D (X) + D (Y).

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:

D (X + C) = D (X).

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

D (X - Y) = D (X) + D (Y).

Литература:

1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.64 – 66, 75 – 94.

2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с. 83 – 141.

Контрольные вопросы:

1. Что называют случайной величиной?

2. Какую величину называют дискретной случайной величиной?

3. Какую величину называют непрерывной случайной величиной?

4. Как задают закон распределения дискретной случайной величины?

5. Что такое многоугольник распределения?

6. Что называют функцией распределения случайной величины?

7. Какими свойствами обладает функция распределения?

8. Какие числовые характеристики случайной величины вы знаете? Дайте им определения, укажите методы их нахождения, перечислите свойства.