Числовые характеристики непрерывной системы двух случайных величин

Зная плотности распределения составляющих Х и У непрерывной двумерной случайной величины (X, У), можно найти их математические ожидания и дисперсии:

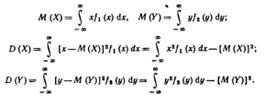
Начальным моментом v_k,s порядка k + s системы (X, Y) называют математическое ожидание произведения X^kY^s:

v_k,s = М[X^kY^s].

Центральным моментом µ_k,s порядка k + s системы (X, Y) называют математическое ожидание произведения отклонений соответственно k-й и s-й степеней:

µ_k,s = М{[X – M(X)]^{k .} [Y –M(Y)]^s}.

Корреляционным моментом µ_ху системы (X, Y) называют центральный момент µ_1,1 порядка 1 + 1:

µ_х,у = М{[X – M(X)] ^. [Y –M(Y)]}.

Коэффициентом корреляции величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

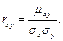
Коэффициент корреляции служит для оценки тесноты линейной связи между X и Y: чем ближе абсолютная величина коэффициента корреляции к единице, тем связь сильнее; чем ближе абсолютная величина коэффициента корреляции к нулю, тем связь слабее.

Коррелированныминазывают две случайные величины, если их корреляционный момент отличен от нуля.

Некоррелированными называют две случайные величины, если их корреляционный момент равен нулю.

Литература:

Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.155 – 179.

Контрольные вопросы:

1. Какие величины называют двумерными?

2. Что представляет собой закон распределения дискретной двумерной случайной величины? В каком виде он может быть представлен?

3. Как зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих?

4. Что представляет собой функцией распределения двумерной случайной величины?

5. Перечислите свойства функции распределения двумерной случайной величины.

6. Что называют плотностью непрерывной двумерной случайной величины?

7. Как отыскать вероятность попадания случайной точки (Х,Y) в область D?

8. Перечислите числовые характеристики непрерывной системы двух случайных величин.