Нормальное распределение.

Распределение с непрерывной случайной величины называется нормальным, если плотность распределения ее описывается формулой:

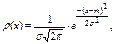
где 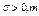– параметры нормального распределения.

Функция распределения случайной величины Х, распределенной по нормальному закону:

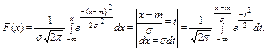
Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию:

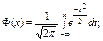
называемую нормальной функцией распределения (функцией Лапласа).

Эта функция неубывающая, непрерывная и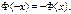

Вероятность попадания случайной величины 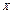, подчиненной нормальному закону распределения, на заданный интервал 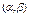, определяется следующим образом:

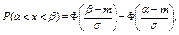
где 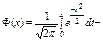функция Лапласа.

Замечание. Имеются специальные таблицы, пользуясь которыми можно найти значения функции Лапласа (Приложение 1).

Вероятность заданного отклонения вычисляется по формуле:

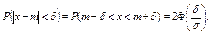
Математическое ожидание и дисперсия соответственно равны:

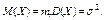
Правило трех сигм: Интервалом практически возможных значений случайной величины 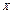, распределенной по нормальному закону, будет интервал .

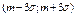Литература:

1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с. 66 – 74.

2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с. 184 – 244.

Контрольные вопросы:

1. Какое распределение случайной величины называется нормальным?

2. Какое распределение случайной величины называют биноминальным?

3. Какое распределение случайной величины называют равномерным?

4. Какое распределение называют распределением Пуассона?