Функция распределения.

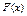Функция распределенияслучайной величины – это функция действительной переменной 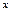, определяющая вероятность того, что случайная величина принимает значение меньше некоторого фиксированного числа 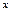, т.е. :

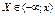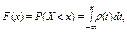
где 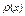– плотность распределения вероятностей.

Плотностью распределения 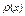непрерывной случайной величиныХ называют предел, если он существует, отношения вероятности попадания случайной величины Х на отрезок 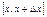, примыкающей к точке 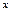, к длине этого отрезка, когда последний стремится к 0, т.е.

.

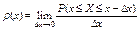При этом вероятность попадания значений случайной величины Х в интервал 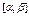равна определенному интегралу от плотности распределения 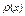по отрезку :

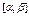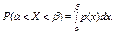
Иногда вместо термина «функция распределения» используют термин «интегральная функция».

Для дискретной случайной величиныфункции распределения вычисляются по формуле:

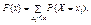
График функции распределения дискретной случайной величины имеет ступенчатый вид. Убедимся в этом на примере.

Пример 4.6. Закон распределения дискретной случайной величины задан следующей таблицей:

Найти функцию распределения.

Решение:

При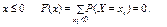

При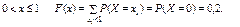

При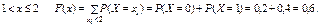

При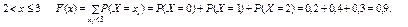

При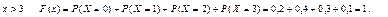

Итак, функция распределения аналитически может быть записана так:

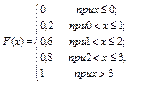
Изобразим график функции .

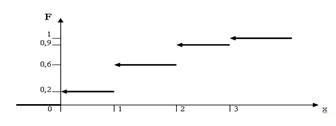
Рис. 4.2. График функции распределения