Приклад виконання розрахунків
2.1 Визначення фізико-механічних властивостей однонаправлених шарів КМ.
Модуль пружності вздовж волокон:
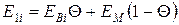
- склопластика:
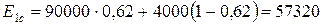 МПа;
МПа;
- вуглепластика:
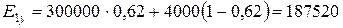 МПа.
МПа.
Модуль пружності поперек волокон:
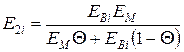
- склопластика:
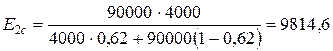 МПа;
МПа;
- вуглепластика:
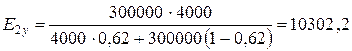 МПа
МПа
Модуль зсуву:
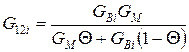
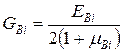 ;
; 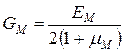 ;
;
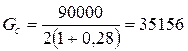 МПа;
МПа;
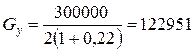 МПа;
МПа;
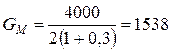 МПа.
МПа.
- склопластика:
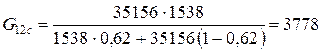 МПа;
МПа;
- вуглепластика:
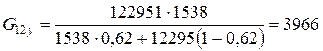 МПа;
МПа;
Коефіцієнт Пуассона при навантаженні по осі 1:
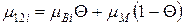
- склопластика:
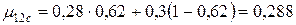 ;
;
- вулепластика:
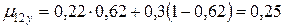 .
.
Коефіцієнт Пуассона при навантаженні по осі 2:
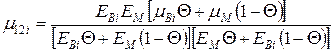
- склопластика:
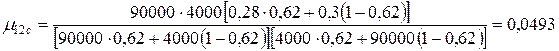 ;
;
- вуглепластика:
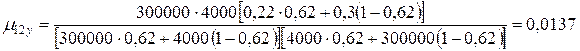 .
.
Перевіряємо виконання рівняння пружного потенціалу:
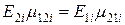
-склопластика:
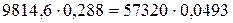
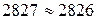
- вуглепластика:
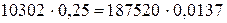
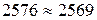
Коефіцієнт лінійного температурного розширення (КЛТР) уздовж волокон:
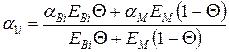
- склопластика:
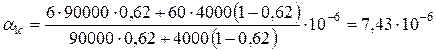 К-1;
К-1;
- вуглепластика:
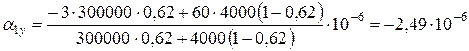 К-1;
К-1;
КЛТР поперек волокон:
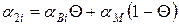
- склопластика:
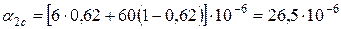 К-1;
К-1;
- вуглепластика:
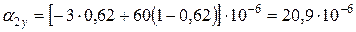 К-1;
К-1;
Міцність на розтягування уздовж волокон:
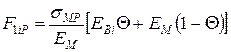 , якщо
, якщо 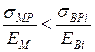 ;
;
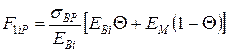 , якщо
, якщо 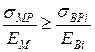 ;
;
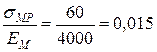 ;
; 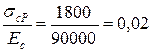 ;
;
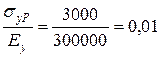 .
.
Тоді
- для склопластика:
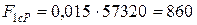 МПа;
МПа;
- для вуглепластика:
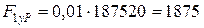 МПа;
МПа;
Міцність на стиснення уздовж волокон:
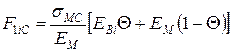 , якщо
, якщо 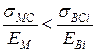 ;
;
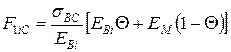 , якщо
, якщо 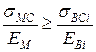 ;
;
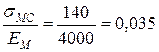 ;
; 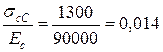 ;
;
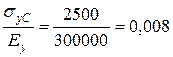 .
.
Тоді:
- для склопластика:
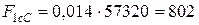 МПа;
МПа;
- для вуглепластика:
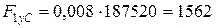 МПа;
МПа;
Міцність на розтягування поперек волокон:
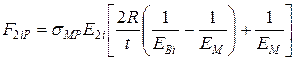 ;
;
де 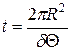 ;
; 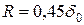
Відношення 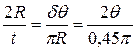
- склопластика:
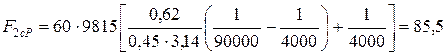 МПа;
МПа;
- вуглепластика:
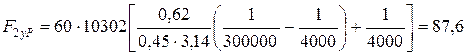 МПа.
МПа.
Міцність на стиснення поперек волокон:
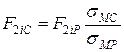
- склопластика:
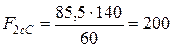 МПа;
МПа;
- вуглепластика:
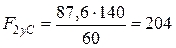 МПа;
МПа;
Міцність на зсув:
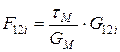 , якщо
, якщо 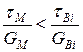 ;
;
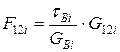 . якщо
. якщо 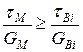 ;
;
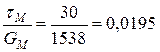 ;
; 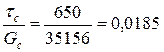 ;
;
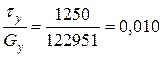 ;
;
- склопластика:
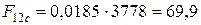 МПа;
МПа;
- вуглепластика:
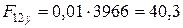 МПа;
МПа;
2.2. Визначення залишкових напружень в компонентах КМ
Напруження у волокнах від температури:
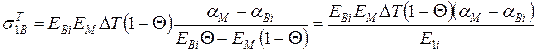
- в скловолокні:
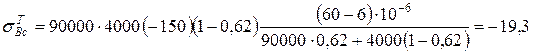 МПа;
МПа;
19,3 МПа < sВс
де sВс – міцність скловолокна при стисненні sВс = 1300 МПа;
- у вуглецевих волокнах вуглепластика:
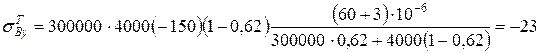 МПа;
МПа;
23 МПа < sВу
де sВу – міцність вуглеволокна при стисненні sВу = 2500 МПа.
Напруга в матриці від температури:
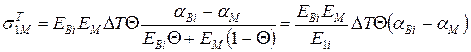
- в склопластику:
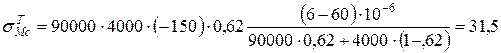 МПа;
МПа;
31,5 МПа < sМр.
Міцність матриці при розтягуванні sМр = 60 МПа;
- у вуглепластику:
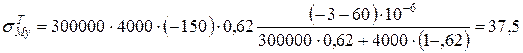 МПа;
МПа;
37,5 МПа < 60 МПа.
Висновок: КМ із заданими параметрами можуть існувати.
2.3. Визначення основних питомих характеристик однонаправлених КМ
Густина КМ:
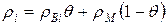 ;
;
- склопластика:
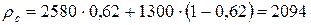 кг/м3;
кг/м3;
- вуглепластика:
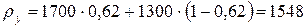 кг/м3;
кг/м3;
Питома жорсткість і міцність
- склопластика:
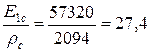
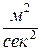 ;
; 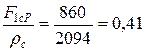
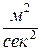 ;
;
- вуглепластика
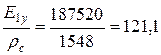
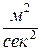 ;
; 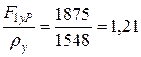
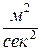 .
.
Для порівняння визначимо аналогічні характеристики, широко використовуваній в машинобудуванні, конструкційної сталі 45: Е = 2×105 МПа; sТ4=в360 МПа; густина 7800 кг/м3.
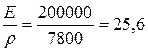
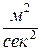 ;
; 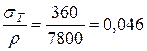
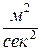 .
.
Висновок: питома жорсткість і питома міцність КМ вище, ніж в сталі. Це означає, що при рівній міцності (жорсткості) конструктивні елементи будуть легшими сталевих. Зниження матеріаломісткості елементів конструкції з різних матеріалів при рівній несучій здатності визначається співвідношенням їх питомих характеристик.
2.4. Визначення величини і напряму головних напружень при заданих умовах зовнішнього напруження (Рис. 2.2)
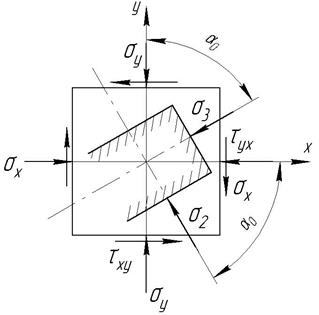
Рис. 2.2. Схема напруженого стану
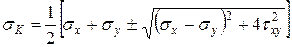 ; К = 1,2,3.
; К = 1,2,3.
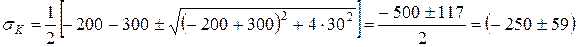 , МПа.
, МПа.
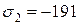 МПа.
МПа.
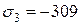 МПа.
МПа.
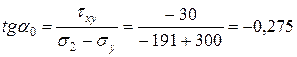 .
.
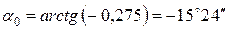 .
.
2.5. На підставі приведених розрахунків формуємо структуру пакету КМ
Оскільки основне навантаження прикладено під гострим кутом до осі у, то заданий кут 30° відкладаємо від цієї осі. Тоді кут армування 3-го і 4-го шарів, відлічуваний від осі х, буде рівний 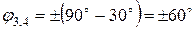 .
.
Загальна товщина 3-го і 4-го шарів 12d0 більше половини сумарної товщини пакету, тому з метою здешевлення матеріалу їх рекомендується виготовляти з більш дешевого склопластика за умови збереження міцності пакету.
Щоб раціонально розташувати 1-й і 2-й шари по відношенню до заданого навантаження (sх, sу), проводимо орієнтовний розрахунок міцності КМ по двох варіантах. Розрахункові формули можна отримати, ураховуючи тільки міцність КМ по напряму армування:
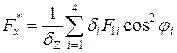 ;
; 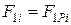 , якщо
, якщо 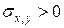 ;
;
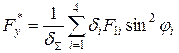 ;
; 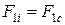 , якщо
, якщо 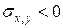 .
.
Варіант І: 1-й шар 4d0 по осі х;
2-й шар 3d0 перпендикулярний осі х
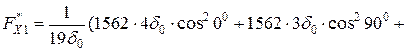
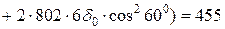 МПа > 200 МПа;
МПа > 200 МПа;
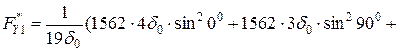
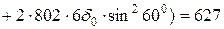 МПа > 300 МПа;
МПа > 300 МПа;
Варіант II: 1-й шар 4d0 перпендикулярний осі х;
2-й шар 3d0 по осі х
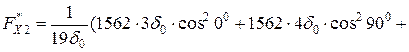
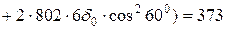 МПа > 200 МПа;
МПа > 200 МПа;
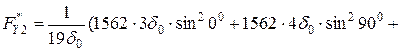
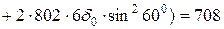 МПа > 300 МПа;
МПа > 300 МПа;
Запас міцності по І варіанту складе:
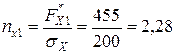 ;
;
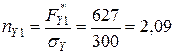 ;
;
Запас міцності по II варіанту складе:
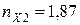 ;
; 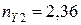
З аналізу отриманих результатів витікає, що КМ по варіанту І більш міцний.
Таким чином, попередній розрахунок показує можливу працездатність матеріалу при заданих нормальних напруженнях. Структура сформованого пакету матеріалу і физико-механічні властивості шарів приведена в таблиці 2.4 і на рис.2.3.
Таблиця 2.4. Физико-механічних властивості шарів пакету КМ
| Номер шару | |||
| Кут укладання jі | ±60 | ||
| Товщина шара, dі, мм | 0,32 | 0,24 | 0,48 |
| Матеріал | В/п | В/п | С/п |
| Е1, МПа | |||
| Е2, МПа | |||
| G12, МПа | |||
| m12 | 0,25 | 0,25 | 0,288 |
| m21 | 0,014 | 0,014 | 0,049 |
| a1×10-6, К-1 | -2,49 | -2,49 | 7,43 |
| a2×10-6, К-1 | 20,9 | 20,9 | 26,5 |
| F1р, МПа | |||
| F1с, МПа | |||
| F2р, МПа | 87,6 | 87,6 | 85,5 |
| F2с, МПа | |||
| F12, МПа | 40,3 | 40,3 | 69,9 |
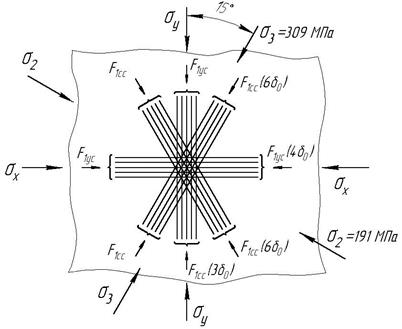
Рис. 2.3 Структура сформованого пакета.
2.6. Рівняння фізичного закону для сформованого пакету шаруватого КМ:
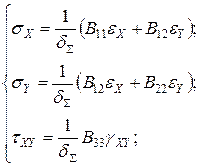
де 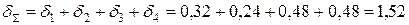 мм, а коефіцієнти матриці жорсткості визначається по формулах:
мм, а коефіцієнти матриці жорсткості визначається по формулах:
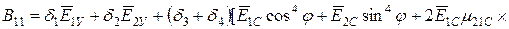
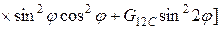 ;
;
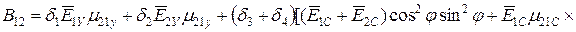
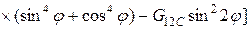 ;
;
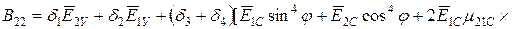
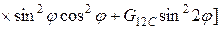 ;
;
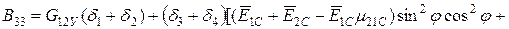
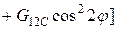 ;
;
де
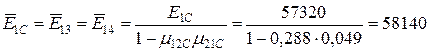 МПа;
МПа;
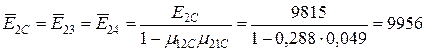 МПа;
МПа;
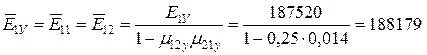 МПа;
МПа;
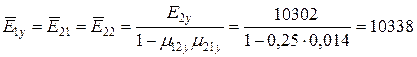 МПа;
МПа;
Підставляючи значення, обчислимо коефіцієнти 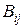 :
:
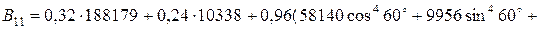
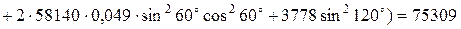 МПа×мм;
МПа×мм;
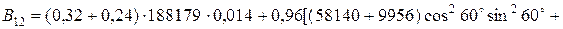
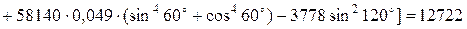 МПа×мм;
МПа×мм;
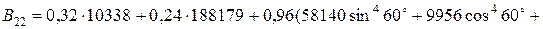
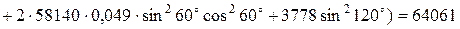 МПа×мм;
МПа×мм;
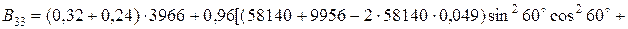
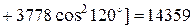 МПа×мм.
МПа×мм.
2.7. Визначення пружних констант шаруватого КМ:
Модуль пружності по осі х:
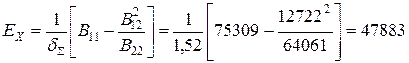 МПа.
МПа.
Модуль пружності по осі у:
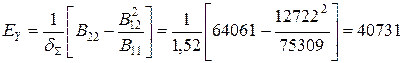 МПа.
МПа.
Модуль зсуву:
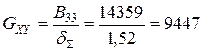 МПа.
МПа.
Коефіцієнти Пуассона:
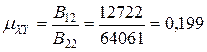 ;
;
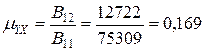 .
.
2.8. Рівняння фізичного закону з урахуванням обчислених значень пружних констант:
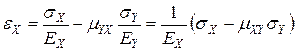 ;
;
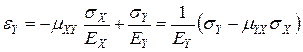 ;
;
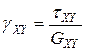 ;
;
Підставляючи значення пружних констант і заданих напружень, визначаємо деформації пакету КМ:
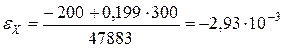 ;
;
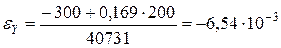 ;
;
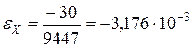 .
.
2.9. Визначаємо коефіцієнти лінійного температурного розширення:
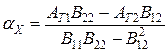 ;
;
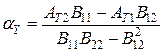 ;
;
Коефіцієнти АТ1 і АТ2 визначаються по наступних формулах:
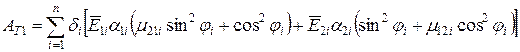 ;
;
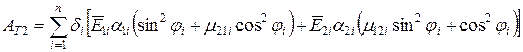 ;
;
Підставляючи значення, отримаємо:
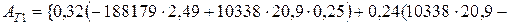
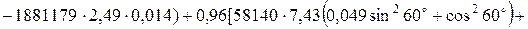
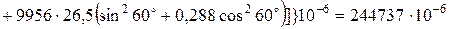 ;
;
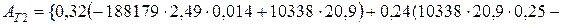
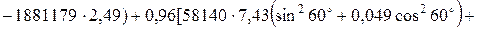
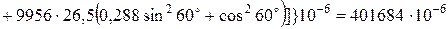 ;
;
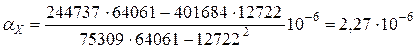 ;
;
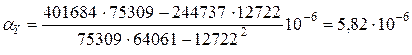 .
.
2.10. Температурні напруження в шарах КМ:
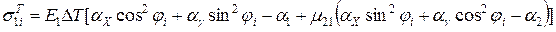 ;
;
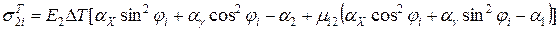 ;
;
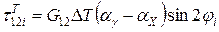 ;
;
Температурні напруження в 1-му шарі:
- вуглепластик:
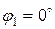 ;
; 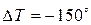 ;
;
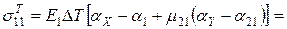
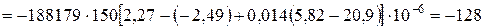 МПа;
МПа;
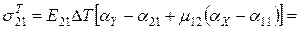
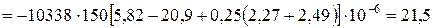 МПа;
МПа;
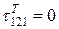 .
.
Температурні напруження в 2-му шарі:
- вуглепластик:
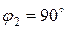 ;
;
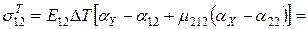
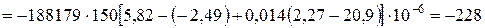 МПа;
МПа;
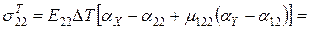
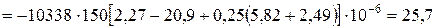 МПа;
МПа;
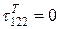 .
.
Температурні напруження в 3-му і 4-му шарах:
- склопластик:
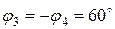 ;
;
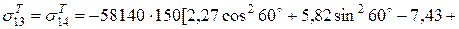
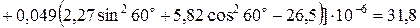 МПа;
МПа;
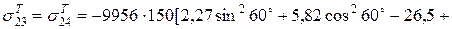
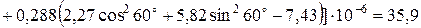 МПа;
МПа;
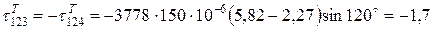 МПа.
МПа.
2.11. Визначаємо деформації шарів в зв'язаній системі координат по формулах:
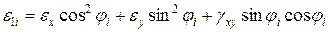 ;
;
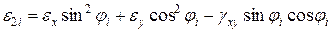 ;
;
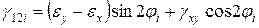 .
.
Для досліджуваної структури:
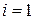 ;
; 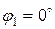 :
:
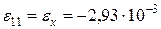 ;
;
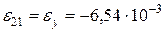 ;
;
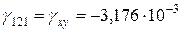 ;
;
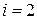 ;
; 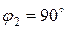 :
:
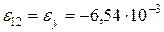 ;
;
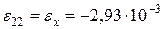 ;
;
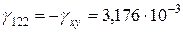 ;
;
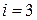 ;
; 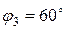 :
:
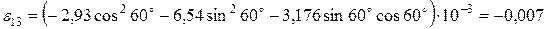 ;
;
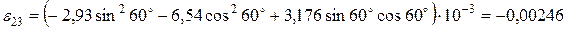 ;
;
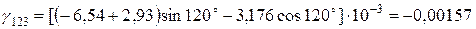 ;
;
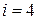 ;
; 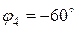 :
:
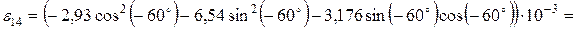
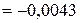 ;
;
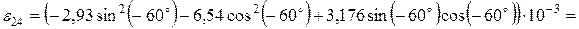
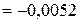 ;
;
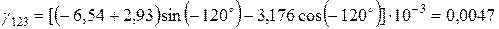 ;
;
2.12. Визначаємо напруження в шарах по формулах:
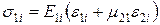 ;
;
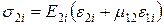 ;
;
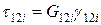 ;
;
В 1-му шарі:
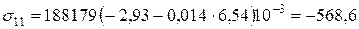 МПа;
МПа;
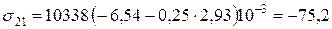 МПа;
МПа;
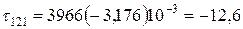 МПа.
МПа.
В 2-му шарі:
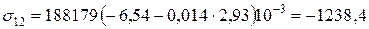 МПа;
МПа;
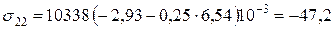 МПа;
МПа;
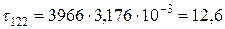 МПа.
МПа.
В 3-му шарі:
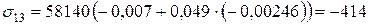 МПа;
МПа;
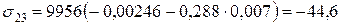 МПа;
МПа;
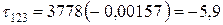 МПа.
МПа.
В 4-му шарі:
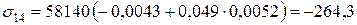 МПа;
МПа;
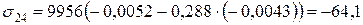 МПа;
МПа;
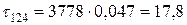 МПа.
МПа.
2.13. На основі даного критерію оцінюємо міцність КМ
По критерію максимальних напружень міцність оцінюється по рівняннях:
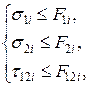 де
де 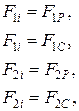
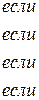
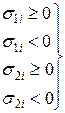
По критерію максимальних деформацій міцність оцінюється по рівняннях
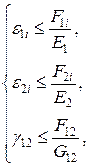 де
де 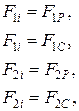
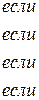
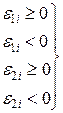
По критерію Мізеса-Хілла міцність оцінюється по рівнянню:
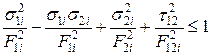 .
.
При цьому значення F1і і F2і визначаються аналогічно критерію максимальних напружень.
Розділивши праву частину будь-якого з критеріїв на ліву, можна отримати значення запасу міцності: шар з найменшим запасом міцності руйнуватиметься першим.
Якщо значення запасу міцності менше одиниці, матеріал не задовольняє умові міцності.
Мінімальним допустимим коефіцієнтом запасу міцності можна також задатися.
Оскільки в даному випадку необхідно використовувати критерій максимальних деформацій, то значення запасу міцності можна розраховувати по формулах:
Для 1-го шару:
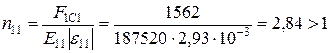 ;
;
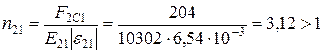 ;
;
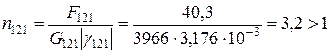 ;
;
Для 2-го шару:
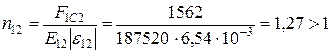 ;
;
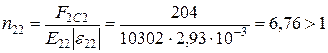 ;
;
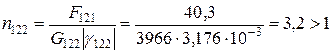
Для 3-го шара:
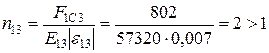 ;
;
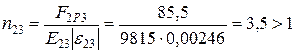 ;
;
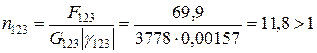
Для 4-го шара:
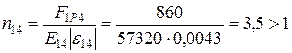 ;
;
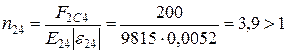 ;
;
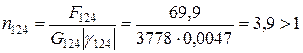
З аналізу отриманих результатів витікає, що даний матеріал задовольняє критерію міцності.
2.14. Визначаємо сумарні напруження в шарах КМ
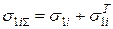 ;
;
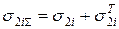 ;
;
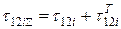 ;
;
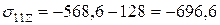 МПа;
МПа;
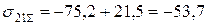 МПа;
МПа;
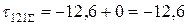 МПа.
МПа.
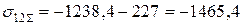 МПа;
МПа;
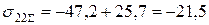 МПа;
МПа;
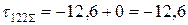 МПа.
МПа.
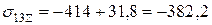 МПа;
МПа;
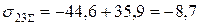 МПа;
МПа;
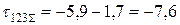 МПа.
МПа.
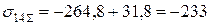 МПа;
МПа;
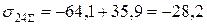 МПа;
МПа;
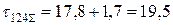 МПа.
МПа.
2.15. Сумарні деформації в шарах можуть бути визначені по формулах:
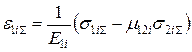 ;
;
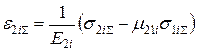 ;
;
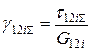 .
.
Тоді
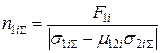 ;
;
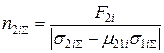 ;
;
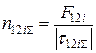 .
.
Підставляючи значення, отримаємо: для 1-го шару
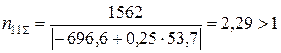 ;
;
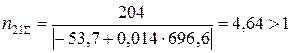 ;
;
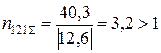 .
.
для 2-го шару
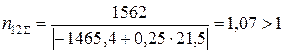 ;
;
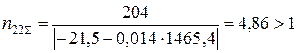 ;
;
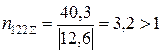 .
.
для 3-го шару
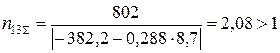 ;
;
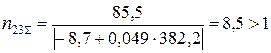 ;
;
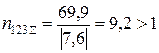 .
.
для 4-го шару
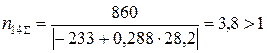 ;
;
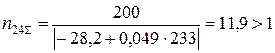 ;
;
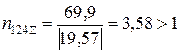 .
.
З аналізу отриманих результатів можна зробити висновок про те, що температурні напруження можуть відігравати як позитивну, так і негативну дію на міцність КМ, але, оскільки загальний запас міцності КМ оцінюється по найбільш слабій ланці, то при заданих умовах навантаження врахування температурних напружень знизило коефіцієнт запасу міцності КМ.
Література
1. Фрегер Г.Е. Игнатьев Б.Б, Меликбекян А.Х. и др. Механика композиционных материалов: Учеб. пособие. - Луганск. Изд-во Восточноукр. ун-та, 1998, - 140с.
2. Гайдайчук В.Е., Карпов В.С. Композиционные материалы в конструкциях летательных аппаратов: Учеб. пособие. - Харьков: ХАИ, 1986. - 76с.
3. Фрегер Г.Е., Игнатьев Б.Б., Коструб В.А., Чесноков В.В. Методические рекомендации к расчетно-проектировочным заданиям и лабораторным работам по курсу "Механика композиционных материалов": Учеб. пособие. - Луганск: Изд-во Восточноукр. гос. ун-та, 1998 - 48 с.
4. Карпинос Д.М., Тучинский Л.И., Вишняков Л.Р. Новые композиционные материалы. - К.: Выща школа, 1997. - 312 с.
5. Физико-механические и эксплуатационные свойства композиционных материалов. Учеб. пособие/ В.Е. Гайдайчук, Я.С. Карпов - Харьков, ХАИ, - 1987. -72с.
6. Композиционные материалы: Учеб. пособие / В.Е. Гайдайчук, Я.С. Карпов, В.Ф. Несвит - Харьков, ХАИ, - 1987. - 53 с.
Дата добавления: 2016-07-27; просмотров: 1347;











