Міцність однонаправлених КМ з безперервними волокнами у напрямі армування

Правило сумішей. Повернемося до моделі однонаправленого трансверсального ізотропного КМ (див. рис. 1.4) і розглянемо характер його деформації (рис. 1.6) під дією розтягуючого навантаження, прикладеного паралельно осі волокон. Для конкретності припустимо, що матриця більш пластична (e_м.гран > e_в.гран) і має менший модуль пружності, ніж волокна (модуль пружності характеризується тангенсом кута нахилу лінійної ділянки кривої до осі деформацій).

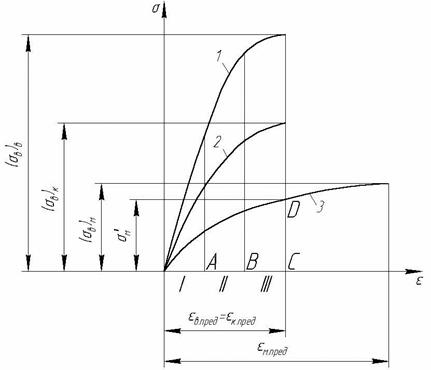
Рис. 1.6. Діаграми розтягування волокон (1), матриці (3) і однонаправленого КМ (2)

В загальному випадку крива 2 розтягування КМ повинна складатися з трьох основних ділянок: І – матриця і волокна деформуються пружно; ІІ – матриця переходить в пружно-пластичний стан, волокна продовжують деформуватися пружно; ІІІ – обидва компоненти системи знаходяться в стані пластичної деформації. Залежно від властивостей складових ділянки ІІ і ІІІ на кривій можуть бути відсутні. Приймемо, що міцність зв'язку на межі розділу волокно – матриця достатня для того, щоб забезпечити сумісну деформацію компонентів аж до руйнування, тобто що e_в = e_м = e_к. Тоді зовнішнє навантаження, яке сприймається армованим матеріалом, дорівнює сумі навантажень, які приходяться на матрицю і волокна, і міркування, аналогічні приведеним в п. 4 при розрахунку модуля пружності Е_хк, дозволяють виразити межу міцності КМ (s_в)_к у вигляді лінійної функції від об'ємної долі волокон V_в:

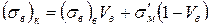. (1.41)

Тут (s_в)_в – середнє значення межі міцності волокон при розтягуванні;

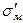– напруження в матриці у момент розриву волокон (рис. 1.6).

Слід чітко уявляти, що 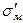– це не межа міцності матриці, а напруження, яке відповідає такій її деформації, яка рівна граничній деформації волокон до руйнування e_в.гран. Щоб визначити величину 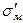, потрібно з точки С, яка відповідає відносній деформації руйнування волокон e_в, поставити перпендикуляр. Ордината точки D перетину цієї прямої з кривою 3 буде рівна 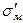. Для пластичних матриць, що незміцнюються, величину 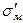можна прийняти приблизно рівною межі текучості матриці.

Рівняння (1.41) називають рівнянням сумішей (правилом сумішей) або рівнянням (правилом) аддитивності. Його часто використовують, оцінюючи міцність однонаправлених композицій по відомих механічних характеристиках компонентів.

На практиці у багатьох випадках допущення, прийняті для виводу рівняння (1.41), порушуються. Руйнуватися волокна можуть не одночасно, а послідовно, через наявність в них дефектів. Найбільш дефектні волокна руйнуються при малих напруженнях, далеких від межі міцності, волокна з меншими дефектами руйнуються при великих напруженнях, а в цілому міцність композиції буде менше розрахованої за правилом сумішей. Те ж можна сказати про випадок, коли матриця має недостатній запас пластичності, що приводить до появи тріщин па межі розділу і в тілі матриці і до передчасного руйнування КМ в цілому.

Проте можливі випадки, коли реальна міцність однонаправленого армованого матеріалу виявляється вищою, ніж та що передбачається рівнянням аддитивності. Наприклад, якщо пластична матриця армована пластичними волокнами, то при розтягуванні КМ зв'язок між волокнами і матрицею утрудняє утворення шийки на волокнах. В результаті волокна в КМ деформуються більш рівномірно, ніж при їх розтягуванні в чистому вигляді (без матриці), оскільки після утворення шийки вся подальша деформація концентрується в ній, викликаючи швидке руйнування. Таким чином, затримка в утворенні шийки зрештою збільшує умовну межу міцності волокон і композиції в цілому. Проте, рівняння (1.41) можна використовувати для оціночних розрахунків, оскільки у багатьох випадках (за умови отримання КМ по оптимальним технологічним режимам) відхилення розрахункових значень міцності від експериментальних невелике.

Оптимальна об'ємна частка волокон. Відповідно до рівняння (1.41) міцність КМ повинна зростати пропорційно об'ємній концентрації волокон V_в. Проте це рівняння здатне описати міцність композицій не при всіх значеннях V_в.

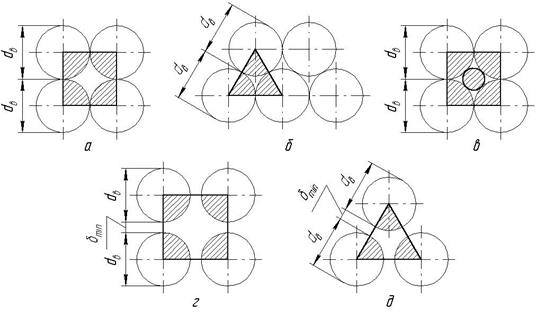
Рис. 1.7. Схеми упаковки однонаправлених волокон при безпосередньому їх контакті (а, б, в) і упаковці з прошарками матриці (г, д)

З одного боку, існують чисто геометричні обмеження, пов'язані з існуванням максимально можливої концентрації циліндричних волокон V_max. Величина V_max залежить від типу упаковки волокон і відповідає такому їх положенню, коли твірні волокон торкаються одна одної. Для тетрагональної упаковки (рис. 1.7, а) V_max = 0,785; для гексагональної (рис. 1.7, б) V_max = 0,907; якщо використовувати волокна різного діаметра і упакувати їх так, як показано на рис. 1.7, в, можна досягти значень V_max » 0,924. Природно, що в реальному матеріалі концентрація волокон буде меншою V_max, оскільки між волокнами майже завжди є прошарок матриці завтовшки d_min (рис. 1.7, г, д). В цих випадках при тетрагональній упаковці (рис.11.7, г)

,

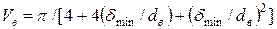при гексагональній (рис. 7, д)

.

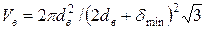Звичайно при V_в > 0,7 ¸ 0,75 КМ проявляє схильність до утворення тріщин і розшарувань, тому такі значення слід вважати верхньою межею для більшості композицій.

З другого боку, при дуже малих V_в крихкі волокна не зможуть обмежити деформацію матриці і руйнуватимуться, а матриця ще буде мати запас міцності і сприймати навантаження. В цьому випадку міцність КМ нижче, ніж міцність неармованої матриці, оскільки введення волокон рівносильно введенню в матрицю ниткоподібних пор. Залежність міцності композиції від об'ємної частки волокон при цьому виразиться формулою

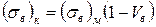(1.42)

де (s_в)_м – межа міцності матриці.

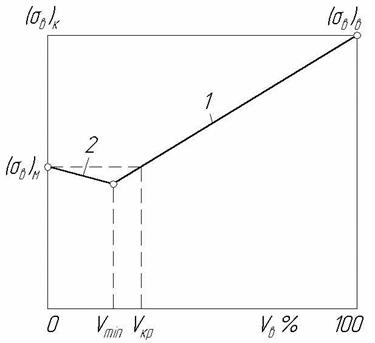
Рис. 1.8. Залежність міцності однонаправлених КМ від об'ємної концентрації волокон: 1 – по рівнянню (1.41); 2 – по рівнянню (1.42 )

Залежність міцності КМ від об'ємної концентрації волокон по рівнянню (1.41) – пряма 1 – і (1.42) – пряма 2 – представлені на рис. 1.8. Об'ємна частка волокон, відповідна точці перетину цих прямих, називається мінімальною об'ємною концентрацією волокон V_min. Їй відповідає мінімальна міцність КМ. Якщо V_в < V_min, міцність композиції зменшується пропорційно збільшенню об'ємної частки волокон, а при V_в > V_min зростає. Значення мінімальної об'ємної частки волокон V_min можна знайти, прирівнюючи вирази (1.41) і (1.42) і вирішуючи отримане рівняння щодо V_min:

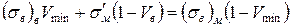. (1.43)

Звідси

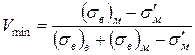. (1.44)

Критичною об'ємною часткою волокон V_кр називають таку об'ємну частку, при якій міцність КМ стає рівній міцності неармованої матриці (рис. 8). Величину V_кр можна розрахувати з умови

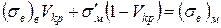. (1.45)

Розв’язуючи рівняння (1.45) щодо V_кр, одержуємо

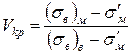. (1.46)

Для більш раціонального армування бажано значення V_кр і V_min мати як можна меншими, щоб досягти зміцнення при невеликій об'ємній частці волокон. На практиці цього добиваються, вводячи в матрицю волокна з межею міцності, що значно перевищує 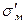(величина 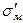, для пластичних матриць звичайно близька до їх границі текучості).

Розрахункові дані про мінімальну об'ємну частку волокон для композицій на основі Аl, Сu, Ni і нержавіючої сталі, армованих проволками з різною границею міцності, приведені в табл. 1.2. При низькій міцності волокон V_min може перевищувати 50 об. %.

Механізм руйнування композицій при V_в > V_min може відрізнятися від такого при V_в < V_min. В разі V_в > V_min міцність всього матеріалу контролюється міцністю волокон і руйнування навіть невеликої їх частини викликає, згідно даної моделі, катастрофічне руйнування матриці і всієї композиції. Якщо ж V_в < V_min і пластична матриця здатна до деформаційного зміцнення при розтягуванні, то розрив волокон не приводить до негайного руйнування матеріалу. У момент розриву волокон напруження падає, але при подальшому навантаженні матриця деформаційно зміцнюється і навантажує зруйновані волокна. В результаті навантаження відновлюється до попереднього рівня. Вся композиція руйнуватиметься тільки після того, як вичерпається запас пластичності матриці. Інакше кажучи, загальна деформація матеріалу контролюється пластичними властивостями матриці. При цьому в процесі навантаження волокна багато разів розриваються по довжині.

Таблиця 1.2 Значення V_min об. % для композицій на основі А1, Сі, Nі і нержавіючої сталі

Механічні властивості матриць, кгс/мм2	Vmin при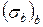
кгс/мм2
Al 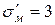;	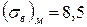8,3	3,2	1,6	0,8
Cu 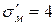;	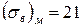25,5	9,8	4,9	2,4
Ni 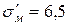;	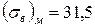39,6		7,3	3,6
Нержавіюча сталь 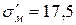;	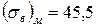53,4	17,8	8,4	4,1

Саме з розривами волокон зв'язаний характерний вид діаграм розтягування армованих систем при V_в < V_min (рис. 1.9, а). Коли волокно розривається, навантаження, яке ним сприймалося, передається матриці, а на діаграмі розтягування з'являється зуб, пропорційний величині цього навантаження. При подальшій деформації в матриці відбувається локальний наклеп і напруження зростає настільки, що вона стає здатною навантажити нові відрізки волокон до їх руйнування в іншому перетині. В результаті діаграма розтягування такої композиції має зубчатий характер, на відміну від систем, в яких об'ємна частка волокон перевищує критичну (рис. 1.9, б).

Питома міцність матеріалу s_пит – це відношення його межі міцності s_в до питомої ваги g

.

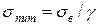Виміряють питому міцність звичайно в сантиметрах, метрах або кілометрах. Аналогічно визначають питомі модулі пружності (питому жорсткість).

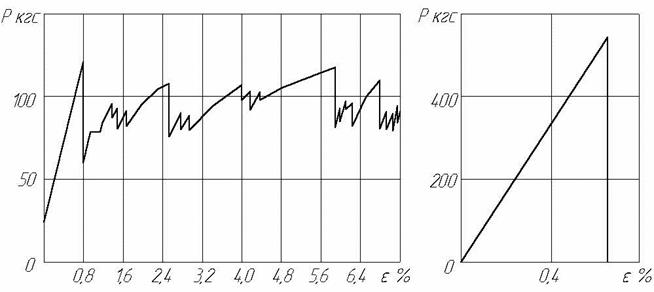
Рис. 1.9. Діаграма розтягування однонаправлених КМ мідь – вольфрамовий дріт:

а – при V_в < V_min (V_в = 10 об.%); б – при V_в > V_min (V_в = 63 об.%)

Питому вагу КМ g_к можна розрахувати по формулі

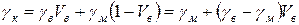(1.47)

де g_м та g_в – питома вага матриці і волокон.

Розділивши обидві частини рівняння (1.41) на вираз (1.47), після нескладних перетворень отримаємо вираз для питомої міцності КМ при V_в ³ V_min:

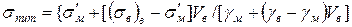. (1.48)

а виконавши ту ж операцію з виразом (1.42), знайдемо формулу для s_пит при V_в < V_min:

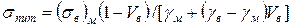. (1.49)

Прирівнявши вирази (1.48) і (1.49) і рішивши отримане рівняння відносно V_в, отримаємо величину V_min, відповідну мінімуму питомої міцності КМ [див. вираз (1.44)]. Значення V_min не залежить від густини матриці і волокон.

Величина V_кр.пит, яка відповідає складу КМ, при якому питома міцність КМ стає рівною питомій міцності неармованої матриці, на відміну від V_min залежить не тільки від характеристик міцності компонентів, але і від їх питомої ваги. Знаходять V_кр.пит, прирівнюючи вираз (1.48) питомої міцності матриці (s_в)_м/g_м:

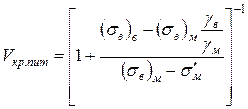. (1.50)

З рівняння (1.50) витікає, що якщо g_в¹g_м то V_кр.пит росте із збільшенням відношення питомої ваги волокон і матриці; якщо ж g_в/g_м = 1, то V_кр.пит = V_кр, визначуваному по формулі (1.46). Коли питомі міцності матриці і волокон однакові, V_кр.пит = 1, і це означає, що при будь-яких значеннях V_в питома міцність КМ не перевищить питомої міцності матриці. Якщо питома міцність матриці більше питомої міцності волокон, то залежність (1.50) втрачає фізичний зміст.