Ілюстрований приклад

Як ілюстрацію викладеного вище матричного підходу використаємо розглянутий нами раніше приклад “споживання – дохід”, дані щодо якого наведені в (9.1.6). Для випадку моделі з двома змінними маємо

, .

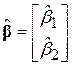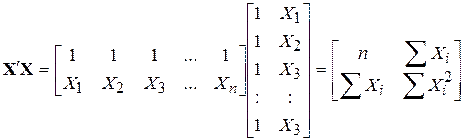Використовуючи дані, наведені в (9.1.6), одержуємо

, .

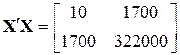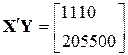Застосовуючи правила для знаходження оберненої матриці, можна переконатися, що

.

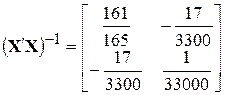Ми бачимо, що результати оцінювання, отримані матричним методом, збігаються з отриманими нами раніше.

Матриця варіації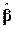

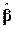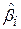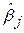Матричний метод дає нам можливість легко отримати не тільки дисперсію (варіацію) для кожного елемента , але й коваріацію між будь-якими двома елементами, скажімо і . Значення цих величин необхідні нам для отримання статистичних висновків.

За визначенням матриця варіації 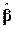є

.

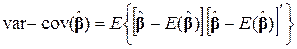У явному вигляді цю матрицю можна подати так:

.

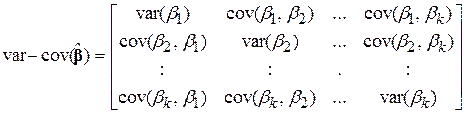(9.3.7)

Можна показати, що матриця варіації 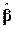може бути отримана за такою формулою:

,

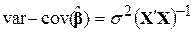(9.3.8)

де 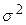– гомоскедастична дисперсія залишків .

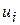У лінійних моделях регресії з двома й трьома змінними незміщена оцінка для 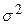обчислювалася, відповідно, за формулами 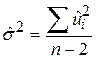і 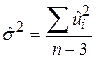. У разі моделі з k змінними формула має вигляд

,

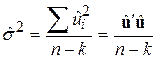(9.3.9)

де (n–k) – кількість степенів вільності.

Хоча теоретично 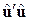може бути підрахована за оцінками залишків, на практиці її зручніше одержувати безпосередньо таким чином.

Пригадавши, що

,

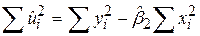у разі трьох змінних

,

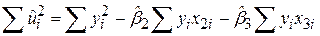та поширюючи цей принцип на випадок моделі з k змінними, одержуємо формулу

,

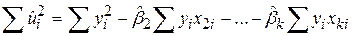(9.3.10)

або в матричних позначеннях

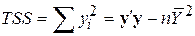;	(9.3.11)
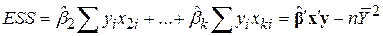,	(9.3.12)

де складова 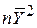відомий як кореляція для середнього.

Отже,

.

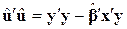(9.3.13)

Оскільки 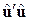отримана, 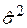може бути легко підрахована за (9.3.9), а потім можна підрахувати матрицю варіацій (9.3.8).

Для нашого прикладу 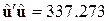. Отже, .

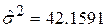Властивості вектора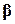

Для випадків моделей із двома й трьома змінними ми знаємо, що оцінки параметрів регресії за МНК є лінійними й незміщеними і в класі лінійних незміщених оцінок вони мають мінімальну дисперсією. Коротше кажучи, оцінки за МНК є якнайкращими лінійними незміщеними оцінками. Ця властивість поширюється й на вектор 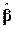, тобто 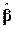- лінійний (кожна з його компонент є лінійна функція від у, залежної змінної). 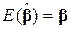, тобто математичне сподівання кожної компоненти вектора 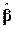дорівнює відповідному елементу істинного вектора 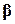і в класі всіх лінійних незміщених оцінок 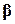МНК-оцінка 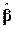має мінімальну дисперсію.

9.4. Коефіцієнт детермінації R² у матричному позначенні

Коефіцієнт детермінації R² визначається так:

.

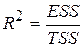У разі двох змінних

,

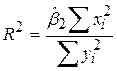а в разі трьох змінних

.

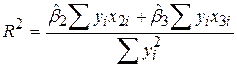Узагальнюючи на випадок k змінних, отримуємо

.

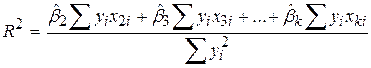(9.4.1)

Рівність (9.4.1) можна переписати як

.

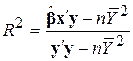(9.4.2)

Для нашого прикладу

, , .

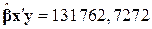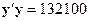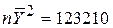Підставляючи ці значення в (9.4.2), одержуємо R²=0,962062.