Ілюстрований приклад: характеристична лінія теорії портфеля
У табл. 4.1 наведені дані за річною нормою прибутку (у %) Afuture Fund, взаємного фонду, завданням інвестиційної політики якого є отримання максимального приросту капіталу, а також ринку портфеля, визначуваного індексом Фішера, за період 1971–1980 рр.
Ми вже згадували, що характеристична лінія в інвестиційному аналізі може бути записана у вигляді
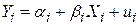 , ,
| (4.1.10) |
де 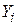 – річна норма прибутку (у %) для Afuture Fund;
– річна норма прибутку (у %) для Afuture Fund;
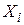 – річна норма прибутку (у %) на ринку портфеля;
– річна норма прибутку (у %) на ринку портфеля;
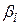 – кутовий коефіцієнт, відомий як бета-коефіцієнт в теорії портфеля;
– кутовий коефіцієнт, відомий як бета-коефіцієнт в теорії портфеля;
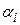 – вільний член у рівнянні регресії.
– вільний член у рівнянні регресії.
У літературі не існує єдиної думки про значення 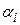 . Деякі емпіричні результати говорять про те, що він позитивний і статистично значимий, інші ж свідчать, що він не відрізняється суттєво від нуля. В останньому випадку ми можемо записати рівняння у вигляді
. Деякі емпіричні результати говорять про те, що він позитивний і статистично значимий, інші ж свідчать, що він не відрізняється суттєво від нуля. В останньому випадку ми можемо записати рівняння у вигляді
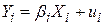 . .
| (4.1.11) |
Це рівняння регресії, що проходить через початок координат. Якщо ми застосуємо рівняння (4.1.11), то отримаємо такі результати:
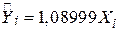 (0,1916)
t = (5,6884) raw
(0,1916)
t = (5,6884) raw 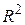 =0,7825. =0,7825.
| (4.1.12) |
Результати свідчать, що 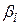 суттєво більше нуля. Інтерпретація отриманих результатів така: при зростанні норми прибутку на ринку портфеля на 1%, норма прибутку для Afuture Fund в середньому зростає на 1,09%.
суттєво більше нуля. Інтерпретація отриманих результатів така: при зростанні норми прибутку на ринку портфеля на 1%, норма прибутку для Afuture Fund в середньому зростає на 1,09%.
Таблиця 4.1.
Річна норма прибутку для Afuture Fund та за індексом Фішера
(ринок портфеля) за 1971–1980 рр.
| Рік | Норма прибутку Afuture Fund, Y | Норма прибутку за індексом Фішера, Х |
| 67,5 | 19,5 | |
| 19,2 | 8,5 | |
| –35,2 | –29,3 | |
| –42,0 | –26,5 | |
| 63,7 | 61,9 | |
| 19,3 | 45,5 | |
| 3,6 | 9,5 | |
| 20,0 | 14,0 | |
| 40,3 | 35,3 | |
| 37,5 | 31,0 |
Чи можна бути впевненим в тому, що модель (4.1.11), а не (4.1.10) є правильною, особливо, якщо врахувати той факт, що не існує сильної попередньої довіри до гіпотези, яка стверджує, що коефіцієнт 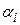 дорівнює нулю? Це можна перевірити, якщо використовувати модель регресії (4.1.10). За цією моделлю ми одержуємо такі результати:
дорівнює нулю? Це можна перевірити, якщо використовувати модель регресії (4.1.10). За цією моделлю ми одержуємо такі результати:
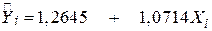 (7,6838) (0,2387)
t = (0,1643) (4,4880)
(7,6838) (0,2387)
t = (0,1643) (4,4880) 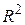 = 0,7157
р = (0,873566) (0,002034) = 0,7157
р = (0,873566) (0,002034)
| (4.1.13) |
Із цих результатів випливає, що ми не можемо відкидати гіпотезу про рівність нулю коефіцієнта 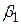 . Це виправдовує використання моделі (4.1.1) – регресії, що проходить через початок координат. Порівняння результатів регресійного аналізу (4.1.12) і (4.1.13) показує, що між ними немає істотної різниці. Слід відзначити лише меншу величину стандартної похибки для коефіцієнта
. Це виправдовує використання моделі (4.1.1) – регресії, що проходить через початок координат. Порівняння результатів регресійного аналізу (4.1.12) і (4.1.13) показує, що між ними немає істотної різниці. Слід відзначити лише меншу величину стандартної похибки для коефіцієнта 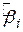 . Це підтримує існуючу думку про більш точне обчислення коефіцієнта
. Це підтримує існуючу думку про більш точне обчислення коефіцієнта 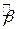 для моделі, що проходить через початок координат. Використовуючи ці дані, можна перевірити, що 95%-й довірчий інтервал для (4.1.12) є (0,6566; 1,5232), а для моделі (4.1.13) цей інтервал є (0,52093; 1,622). Другий довірчий інтервал вужчий, ніж перший, що свідчить про більшу точність визначення коефіцієнта
для моделі, що проходить через початок координат. Використовуючи ці дані, можна перевірити, що 95%-й довірчий інтервал для (4.1.12) є (0,6566; 1,5232), а для моделі (4.1.13) цей інтервал є (0,52093; 1,622). Другий довірчий інтервал вужчий, ніж перший, що свідчить про більшу точність визначення коефіцієнта 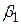 за моделлю (4.1.12).
за моделлю (4.1.12).
Дата добавления: 2016-07-27; просмотров: 1795;











