Модулі пружності однонаправлених армованих КМ

Розглянемо, як розрахувати модулі пружності армованих КМ по відомих пружних характеристиках і об'ємних концентраціях його компонентів. Зупинимося на найпростішому випадку КМ – системі з паралельно укладених в одному напрямі армуючих елементів, зв'язаних між собою матричними прошарками (рис. 1.4). Пластини (моношари) таких матеріалів – основа для отримання різних шаруватих КМ, а по відомих характеристиках однонаправлених матеріалів можна розраховувати властивості композицій з різною орієнтацією волокон в суміжних шарах. Тому надалі основну увагу будемо надавати властивостям однонаправлених композицій. Такі матеріали трансверсально ізотропні.

Основні допущення, що приймаються в розрахунку, зводяться до того, що волокна і матриця – ізотропні пружні матеріали, які при навантаженні композиції деформуються спільно (це забезпечується наявністю між ними жорсткого зв'язку).

Модуль нормальної пружності Е_хк (у напрямі осей волокон). Навантажимо дану пластину силою Р_х. При цьому відносна деформація e_хк композиції у напрямі осі х через спільність деформацій матриці і волокон буде рівна деформації матриці e_хм і волокон e_хв:

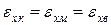. (1.23)

Сума сил, діючих на матрицю Р_хм і на волокно Р_хв, рівна загальній силі Р_х:

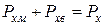. (1.24)

Скориставшись тим, що силу можна представити як добуток напруження на площу поперечного перетину, рівність (1.24) перепишемо у вигляді

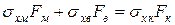(1.25)

де s_хм, s_хв і s_хк – растягуючі напруження відповідно в матриці, волокні і всій композиції у напрямі осі х;

F_м, F_в і F_к – площі поперечних перетинів матриці, волокна і композиції відповідно.

Розділивши обидві частини рівності (1.25) на Р_к, отримаємо

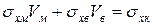(1.26)

де V_м, V_в – об'ємна частка відповідно матриці, волокна в композиційному матеріалі;

;

; .

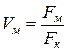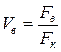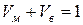Закон Гука для одноосного напруженого стану дозволяє записати наступне:

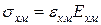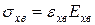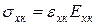; ; . (1.27)

Тут Е_хм, Е_хв і Е_хк – модулі Юнга відповідно матриці, волокон і композиції у напрямі х. Оскільки матеріали матриці і волокон прийняті ізотропними, то надалі індекси в характеристик цих матеріалів, що вказують напрям, будемо опускати і використовувати тільки індекси „м” і „в”.

Якщо замість напружень в рівняння (1.26) підставити їх вирази з рівняння (1.27) і скористатися умовою (1.23), можна отримати вираз

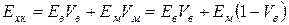. (1.28)

Вираз (1.28) дозволяє оцінити величину модуля нормальної пружності однонаправлений КМ у напрямі армування по відомих концентраціях і модулях пружності матриці і волокон.

Модуль пружності Е_ук (в напрямі, перпендикулярному до осі волокон). Розглянемо поведінку моделі (рис. 1.4) при навантаженні її силою Р_у, перпендикулярною до поздовжньої осі волокон. В цьому випадку напруження в кожному з компонентів КМ будуть однаковими:

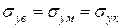(1.29)

а абсолютна деформація D_ук всій композиції буде рівна сумі абсолютних деформацій матриці D_ум і волокон D_ув:

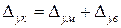. (1.30)

Абсолютна деформація D пов'язана з відносною e співвідношенням D = le, де l – довжина елемента, що деформується. Підстановка цього співвідношення в рівність (1.30) дає

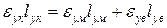(1.31)

де e_ук, e_ум і e_ув – відносні деформації відповідно композиції, матриці і волокна в напрямі осі у;

l_ук, l_ум, l_ув – відповідно довжина даного елемента КМ, сумарна довжина матричних прошарків і волокон в напрямі у.

Якщо для простоти прийняти, що перетини волокон прямокутні, то

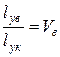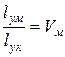; . (1.32)

Розділивши обидві частини рівняння (1.31) на l_ук, з урахуванням залежності (1.32) отримаємо

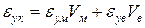. (1.33)

Виразивши за допомогою закону Гука деформації у виразі (1.33) через відповідні напруження і модулі пружності (e=s/E) і взявши до уваги умову (1.29), прийдемо до співвідношення, що дозволяє оцінити модуль пружності композиції в напрямі, перпендикулярному до поздовжньої осі волокон:

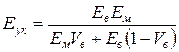. (1.34)

Коефіцієнт Пуассона. За визначенням коефіцієнт Пуассона композиції

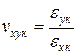. (1.35)

При навантаженні силою Р_х деформацію e_ук можна розрахувати із співвідношення (1.33) з урахуванням того, що ; ;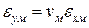

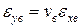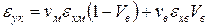. (1.36)

Підставляючи у формулу (1.35) вираз (1.36) і використовуючи умову (1.28) одержуємо формулу для визначення коефіцієнта Пуассона:

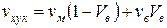. (1.37)

Модуль зсуву. При навантаженні даної моделі КМ дотичними напруженнями t_ху (рис. 1.5) навантаження сприймається матрицею і волокнами послідовно, через що величини дотичних напруг в матриці t_хум і волокнах t_хув однакові:

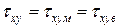. (1.38)

При цьому деформація зсуву КМ, по аналогії з виразом (1.33), визначається співвідношенням

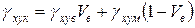. (1.39)

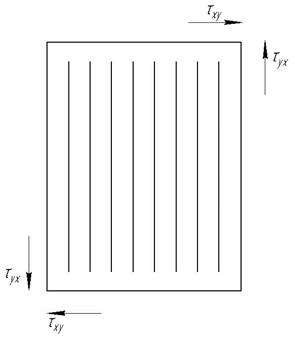
Рис. 1.5. Схема навантаження однонаправленого КМ дотичними напруженнями

Оскільки поведінка всіх компонентів розглядається в межах пружних деформацій, можна скористатись законом Гука для зсуву

.

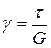Після підстановки його в рівняння (1.39), з урахуванням рівняння (1.38) отримаємо

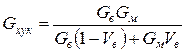(1.40)

Як уже відмічалось, чотири пружні константи – Е_хк, Е_yк, G_хук і v_хук – повністю описують поведінку моделі однонаправленого армованого матеріалу при плоскому напруженому стані.

Слід зазначити, що отримані співвідношення (1.28), (1.34), (1.37) та (1.40) можна розглядати тільки як наближені, оціночні, оскільки модель для їх розрахунку дуже ідеалізована. Технологічні дефекти, неоднорідності в розподілі волокон за об'ємом, кривизна їх перетинів, розорієнтація і розкид властивостей компонентів приводять до того, що реальні характеристики армованих композицій відрізняються від розрахункових. Тому для паспортизації КМ звичайно використовують експериментально визначені пружні константи.