Закон Гука для анізотропних тіл
Закон Гука встановлює зв'язок між пружними напруженнями s, діючими на тіло, і деформаціями e, викликаними цими напруженнями. Для одноосного розтягу або стиску ізотропного тіла, на яке діє тільки одна сила, закон Гука записується у вигляді
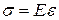 . (1.1)
. (1.1)
Коефіцієнт пропорційності Е називають модулем пружності при одноосному розтягуванні або модулем нормальної пружності, або модулем Юнга. Це константа ізотропного матеріалу, що характеризує його жорсткість.
При одноосному розтягу матеріалу разом із збільшенням його довжини у напрямі дії сили (наприклад, по осі х) зменшуються поперечні розміри уздовж двох інших осей (у і z). Відношення відносних деформацій зразка в поперечному і подовжньому напрямах називається коефіцієнтом Пуассона v:
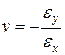 . (1.2)
. (1.2)
По аналогії з розтягом зв'язок між дотичними напруженнями t і відповідними пружними деформаціями зсуву g можна записати співвідношенням
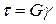 , (1.3)
, (1.3)
де G – модуль пружності при зсуві (модуль зсуву).
При гідростатичному стиску ізотропних тіл закон Гука встановлює пряму пропорційність між гідростатичним тиском р і зміною об'єму  :
:
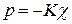 (1.4)
(1.4)
де К – модуль об'ємної деформації.
Справедливий закон Гука тільки при порівняно малих величинах напружень і деформацій, коли ще немає необоротних пластичних деформацій і матеріал поводиться як абсолютно пружне тіло.
Співвідношення (1.1) і (1.3) характеризують, зв'язок між напруженням і деформацією в одному і тому ж напрямі. Але до тіла одночасно можуть бути прикладені напруження в двох або трьох взаємно перпендикулярних напрямах. В результаті мають справу відповідно з плоским і з об'ємним напруженими станами матеріалу.
Проте навіть під дією одноосного розтягу або стиску тіло деформується в трьох взаємно перпендикулярних напрямах х, у і z, тобто одноосний (лінійний) напружений стан приводить до виникнення тривісного, або об'ємного, деформованого стану. Можлива і така комбінація сил, при якій тіло буде знаходитися в плоскому або одноосному деформованому стані.
В загальному випадку зв'язок між напруженнями і деформаціями для ізотропного тіла встановлює узагальнений закон Гука, який в позначеннях, використовуваних в техніці (технічних позначеннях), має наступний вигляд:
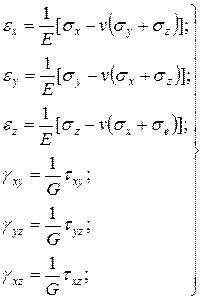 (1.5)
(1.5)
Тут sх, sу, sz – нормальні напруження в трьох взаємно перпендикулярних напрямах х, у і z;
eх, eу, ez – відносні деформації у напрямі відповідних осей координат (осьові деформації);
tху, tуz, txz – дотичні напруження;
gху, gуz, gxz – кутові (зсувові) деформації.
Пружні константи E, G, v і K зв'язані між собою співвідношеннями
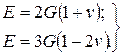 (1.6)
(1.6)
Тільки дві з чотирьох констант незалежні; дві інші можна обчислити із співвідношення (1.6) по цих двох відомих. Іншими словами, щоб отримати повну інформацію про співвідношення між напруженим і деформованим станами пружного ізотропного тіла, достатньо знати його пружні константи.
Для анізотропних тіл закон Гука встановлює пропорційність між кожним компонентом тензора деформацій і всіма шістьма компонентами тензора напружень (тензором називають сукупність математичних величин, що перетворюється при повороті осей координат по певних лінійних законах і які володіють рядом властивостей, загальних для цих величин).
Напружений стан в будь-якій точці навантаженого тіла характеризується дев'ятьма величинами, які утворюють тензор напружень, який записують у вигляді
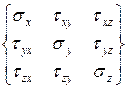 . (1.7)
. (1.7)
Тут три компоненти (sх, sу, sz) позначають нормальні напруження, інші шість – дотичні. Часто нормальні і дотичні напруження позначають однією буквою sik і розрізняють їх по індексах: компоненти з двома однаковими індексами (s11, s22, s33) відповідають нормальним, а з різними індексами – дотичним напруженням. В цьому випадку говорять, що тензор напружень записаний в нумерованих осях 1; 2; 3:
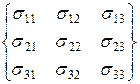 . (1.8)
. (1.8)
З дев'яти компонентів тензора напружень тільки шість незалежні; компоненти, симетричні щодо головної діагоналі тензора s11 – s33, рівні між собою, тобто s12=s21; s13=s31; s23=s32.
Деформований стан в точці описується за допомогою тензора деформацій, який в технічних позначеннях має вигляд
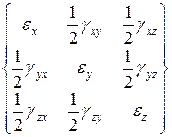 (1.9)
(1.9)
а в нумерованих осях записується таким чином:
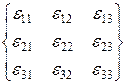 . (1.10)
. (1.10)
У виразі (1.9) компоненти ex, ey і ez – лінійні, а інші шість компонентів – описують деформації зсуву. При цьому
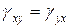 ;
; 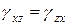 ;
; 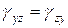 . (1.11)
. (1.11)
В рівнянні (1.10) відповідно
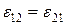 ;
; 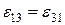 ;
; 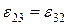 . (1.12)
. (1.12)
В літературі використовують три форми запису закону Гука для анізотропних середовищ – тензорну, матричну і технічну.
В скороченій тензорній формі закон Гука можна представити так:
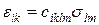 . (1.13)
. (1.13)
Тут індекси i, k, l, m приймають послідовно значення 1; 2 і 3; eik, позначає відносну лінійну деформацію при i=k і кутову при i¹k (e11, e22, і e33 – лінійні деформації, відповідні деформаціям eх, ey і ez уздовж осей х, y і z; e12=e21; e13=e31; e23=e32 – кутові деформації, відповідні деформаціям 1/2 gху, 1/2 gхz і 1/2 gуz); slm – нормальні напруження при l=m і дотичні при l¹m (наприклад, при l=1, m=1 s11 позначає нормальне напруження, діюче уздовж осі x, при l=2, m=2 s22, позначає те ж у напрямі осі y; при l=1, m=2 s12 позначає дотичне напруження, відповідне tху); ciklm – коефіцієнти пружності анізотропного тіла, створюючі тензор четвертого рангу.
Запис (1.13) припускає, що для отримання значень eik. слід підсумувати добутки сiklm slm по індексах, що зустрічаються двічі, тобто по індексах l і m. Знак підсумовування при цьому опускається. Запис (1.13) відповідає наступному запису з використанням знаків підсумовування:
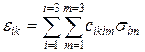 . (1.14)
. (1.14)
Якщо хочуть детально розписати вираз для відносного подовження у напрямі осі х, приймають і=k=1. Тоді
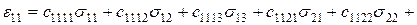
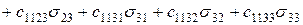 .
.
Вираз для кутової деформації в площині ху виходить з рівняння (1.13), якщо покласти і=1, k=2:
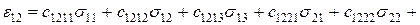
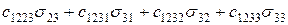 .
.
Тензорний запис (1.13) вимагає для обчислення всіх деформацій знати 81 коефіцієнт сiklm. Але насправді, як доводить теорія пружності, з 81 коефіцієнта незалежними і відмінними від нуля можуть бути тільки 21. Так, щоб визначити всі компоненти тензора деформацій, в загальному випадку анізотропного тіла потрібно знати 21 коефіцієнт пружності.
Вираз (1.13) встановлює залежність пружних деформацій eik від напружень slm. Справедливо і зворотне співвідношення, записане в тензорній формі:
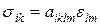 , (1.15)
, (1.15)
яке встановлює залежність напружень від деформацій. Правила підсумовування тут такі ж, як і у формулі (1.13).
Тензорний запис зручний для обчислення пружних коефіцієнтів анізотропних матеріалів в напрямах, не співпадаючих з головними осями симетрії, оскільки такий запис дозволяє використовувати правила тензорного числення при повороті координатних осей. Його доцільно застосовувати, коли розглядається плоский або об'ємний напружений стан анізотропного тіла з низькою симетрією.
В загальному випадку анізотропного матеріалу пружні сталі, які створюють тензор четвертого рангу, для довільно орієнтованих напрямів можна розрахувати відповідно до правил перетворення тензорних величин при повороті осей координат по наступній формулі:
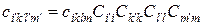 . (1.16)
. (1.16)
Тут буквами C з двома індексами позначені направляючі косинуси кутів між новою і старою системами прямокутних координат (табл. 1.1). Перший індекс відповідає номеру нової осі, а другий – номеру старої. Першою вважається вісь х, другою – у і третьою – z. Наприклад, С11 – це косинус кута між новою віссю х' і старою х, С12 – між новою віссю х' і старою y. С32 – між новою віссю z' і старою y і т.п. Кути між позитивними напрямами осей можуть змінюватися від 0 до 180°, тому кожне значення C однозначно визначає кут.
Таблиця 1.1 Направляючі косинуси
| x | Y | z | |
| х' | C11 | C12 | C13 |
| у' | C21 | C22 | C23 |
| z' | C31 | C32 | C33 |
Формула (1.16) – скорочений тензорний запис. Вона припускає підсумовування по всіх індексах, що двічі зустрічаються в правій частині. Індекси послідовно пробігають значення 1; 2 і 3.
Разом з тензорним записом закону Гуrа застосовується матрична форма запису:
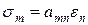 (1.17)
(1.17)
і
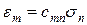 . (1.18)
. (1.18)
Від тензорного запису можна перейти до матричного, якщо два індекси об'єднати в один, пробігаючий значення 1, ...., 6. Схема заміни індексів наступна:
тензорні позначення – 11 22 33 23;32 31;13 12;21
матричні позначення – 1 2 3 4 5 6.
Матричний запис (1.18), наприклад, детально можна розписати так:
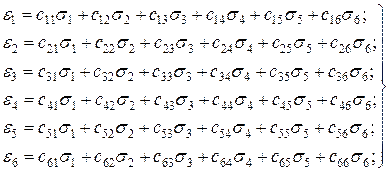 (1.19)
(1.19)
При заміні тензорних позначень на матричні коефіцієнти aiklm переходять в amn sik – sm; перехід від eik до em виконується за правилом
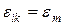 , якщо m=1; 2 або 3;
, якщо m=1; 2 або 3;
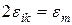 , якщо m=4; 5 або 6;
, якщо m=4; 5 або 6;
при переході від сiklm до сmn вводяться наступні множники:
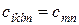 , якщо m і n рівні 1; 2 або 3;
, якщо m і n рівні 1; 2 або 3;
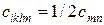 , якщо m або n рівно 4; 5 або 6;
, якщо m або n рівно 4; 5 або 6;
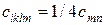 , якщо m і n рівні 4; 5 або 6.
, якщо m і n рівні 4; 5 або 6.
З 36 коефіцієнтів, що входять в запис (1.19), коефіцієнти сmn=сnm, і фактично достатньо 21 коефіцієнта для отримання повної інформації про поведінку анізотропною тіла в межах пружності.
Технічна форма запису закону Гука використовує технічні постійні пружності – модулі Юнга, зсуву, об'ємного стиснення і коефіцієнти Пуассона. Звичайно її застосовують, описуючи пружну поведінку анізотропних тіл з достатньо високою симетрією.
Наприклад, для ортотропного матеріалу закон Гука в технічних позначеннях можна записати так:
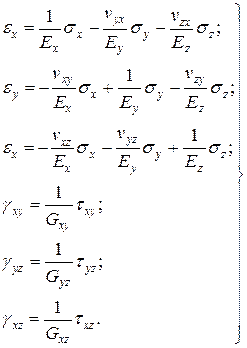 (1.20)
(1.20)
Тут і надалі прийняті наступні позначення:
Е – модулі нормальної пружності при розтягуванні або стисненні у напрямі осі, вказаної в індексі;
G – модулі зсуву при дії дотичних напружень по площинах, вказаних в індексах;
v – коефіцієнти поперечної деформації (коефіцієнти Пуассона) у напрямі першої з осей, вказаних в індексі, при дії нормальних напружень у напрямі другої осі.
З 12 пружних коефіцієнтів, що входять у вирази (1.20), 9 незалежні. Зазвичай в якості незалежних констант приймають 3 модулі пружності – Ех, Еy, Еz, 3 модулі зсуву – Gxy, Gxz і Gyz і 3 коефіцієнти Пуассона – vxy, vyz, vzx. Решта 3 коефіцієнта Пуассона розраховують із співвідношень
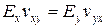 ;
; 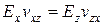 ;
; 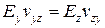 . (1.21)
. (1.21)
Пружні постійні ciklm ортотропного тіла пов'язані з технічними модулями пружності такими співвідношеннями:
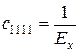 ;
; 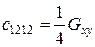 ;
; 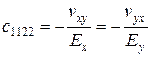 ;
;
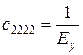 ;
; 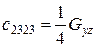 ;
; 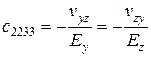 ;
;
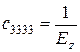 ;
; 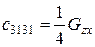 ;
; 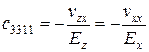 ;
;
Для анізотропних матеріалів з більш високою симетрією кількість незалежних пружних констант зменшується. Наприклад, в трансверсально ізотропних тілах напряму х і y рівноцінні, тому для таких тіл справедливі рівності
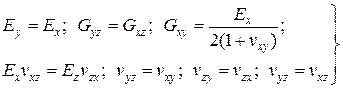 (1.22)
(1.22)
і незалежними залишаються тільки 5 пружних констант – Ех, Еz, Gxz, vxz, vxy. Якщо на матеріал діють тільки два взаємно перпендикулярних напруження sх і sy, а sz=0, то ортотропне тіло можна охарактеризувати чотирма постійними: Ех, Еу, Gху і vxy.
Дата добавления: 2016-07-27; просмотров: 1352;











