Міцність при розтягуванні КМ, армованих дискретними волокнами
Критична довжина волокон.Розглянуті в пункті 1.5 формули для визначення міцності КМ справедливі лише тоді, коли армуючі волокна безперервні. Якщо ж КМ армований короткими (дискретними) волокнами, слід враховувати так званий „кінцевий ефект”, пов'язаний з концентрацією напруги у кінців волокон, який позначається на величині міцності КМ в цілому.
У КМ, армованому паралельно укладеними короткими волокнами довжиною l і навантаженому уздовж волокон, навантаження передається волокнам за рахунок дотичної напруги на поверхнях розділу між волокнами і матрицею. Залежно від довжини волокон можливі два випадки поведінки їх в КМ. При значеннях l, менших певної критичної довжини lкр, що розтягують напругу у волокнах опиняються недостатніми для того, щоб викликати їх руйнування, волокна витягуються з матриці і міцність їх недовикористання.
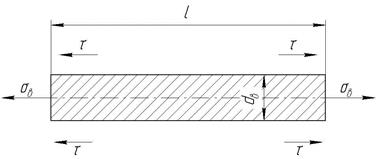
Рис. 1.10. Сили, що діють на волокно при розтягуванні армованої композиції
При l > lкр волокна руйнуються від розтягуючої напруги, при цьому чим більше l, тим велику міцність має КМ в цілому.
Критичною довжиною волокна lкр називають мінімальну довжину волокон, при якій вони руйнуються в КМ. Величина lкр залежить від міцності зв'язку між матрицею і волокнами і діаметру волокон. Якщо приблизно прийняти, що по довжині волокна дотична напруга розподілена рівномірно (це близько до поведінки КМ з ідеально пластичними матрицями), то значення l/lкр можна знайти з умови рівноваги дотичних і нормальних сил, що діють на волокно (рис. 1.10):
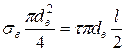 . (1.51)
. (1.51)
Тут t – дотична напруга на межі розділу волокно – матриця;
sв – нормальна розтягуюча напруга у волокні;
l і dв – довжина і діаметр волокна.
При l = lкр у момент руйнування КМ дотична напруга рівна міцності зсуву межі розділу tг.р, а розтягуюча напруга у волокнах – їх межі міцності (sв)в. Тому
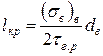 . (1.52)
. (1.52)
Таким чином, критична довжина волокон збільшується із зменшенням міцності межі розділу і збільшенням міцності волокон і їх діаметру. У КМ з пластичною матрицею максимальна дотична напруга на межі розділу може лімітуватися межею текучості матриці.
Зазвичай в розрахунках використовують безрозмірну величину, а не абсолютне значення lкр, оскільки вона не залежить від діаметру волокон. Користуючись формулою (1.52), цю величину можна оцінити по відомих (sв)в і tг.р. Розрахунок показує (табл. 1.3), що для армованих металів lкp/dв лежить в межах 10 – 250, для пластиків ця величина може дорівнювати 350 і більш.
З підвищенням температури величина tг.р зменшується, тому КМ, призначені для роботи при високих температурах, повинні мати волокна більшої довжини, чим низькотемпературні матеріали. Точне значення міцності зв'язку між арматурою і матрицею не піддається аналітичному розрахунку, тому його визначають експериментально.
Таблиця 1.3 Значення lкp/dв для КМ з різною міцністю межі розділу tг.р кгс/мм2 і трьома рівнями міцності волокон (sв)в кгс/мм2
| Матеріал матриці | tг.р | (sв)в | lкp/dв |
| Смола | 1,0 | ||
| Аl | 1,4 | ||
| Аg | 2,8 | ||
| Сu, Ni | 3,5 |
Правило сумішей для КМ з дискретними волокнами. Міцність у напрямі армування для КМ, зміцнених паралельними відрізками волокон, можна оцінити за правилом сумішей з урахуванням „кінцевого ефекту”. Розглянемо, який вплив робить довжина волокон на величину середньої розтягуючої напруги 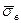 в них.
в них.
1. l< lкр. В цьому випадку у міру збільшення довжини волокна росте як максимальна розтягуюча напруга (діє посередині волокна), так і середня розтягуюча напруга 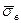 у волокнах, яку можна розрахувати по формулі
у волокнах, яку можна розрахувати по формулі
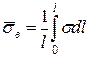 .
.
Припустимо, що нормальна напруга у волокнах росте від кінців волокна до його середини по лінійному закону (рис. 1.11). Тоді при l < lкр епюра напруги має вигляд, зображений на волокнах з довжинами l1 і l2. Максимальна напруга відмічена штриховою лінією, середнє – штрих-пунктирною. В цьому випадку максимальна напруга у волокнах не досягає їх межі міцності і середня нормальна напруга
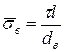 .
.
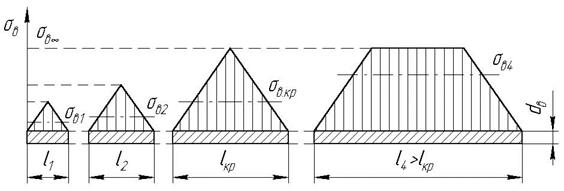
Рис. 1.11. Епюри розтягуючих напруг у волокнах різної довжини
Руйнуються такі КМ за рахунок витягування волокон. При цьому середня розтягуюча напруга у волокнах у момент руйнування КМ рівна 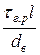 і рівняння аддитивності (1.41) приймає вигляд
і рівняння аддитивності (1.41) приймає вигляд
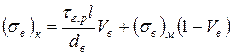 . (1.53)
. (1.53)
Таким чином, якщо l<lкр, то міцність однонаправлених КМ зростає пропорційно об'ємній частці волокон, відношенню l/dв, міцності межі розділу і міцності матриці, залишаючись при цьому менше міцності КМ, армованих безперервними волокнами.
2. l ³ lкр Коли довжина волокна стає рівною lкр, максимальна нормальна напруга в середній частині волокна досягає значення, рівного розтягуючій напрузі sв¥ в нескінченно довгому волокні. При подальшому збільшенні l рівень максимальної напруги у волокні залишається незмінним (рівним sв¥), але збільшуються ділянки волокон, на яких діє ця напруга. Отже, росте і середня напруга, тобто для волокон завдовжки l1 < l2 < lкр < l4 має місце співвідношення 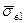 <
< 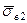 <
< 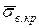 <
< 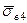
Припустимо, що величина середньої розтягуючої напруги у волокні на кінцевих ділянках завдовжки 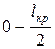 рівна Wsв¥, де W – коефіцієнт, менший 1. Ці ділянки складають частину загальної частки волокон, рівну
рівна Wsв¥, де W – коефіцієнт, менший 1. Ці ділянки складають частину загальної частки волокон, рівну 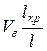 Частка ділянок, на яких діє напруга sв, складає
Частка ділянок, на яких діє напруга sв, складає 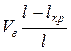 .
.
Напруга, усереднена по всій довжині волокон, можна визначити таким чином:
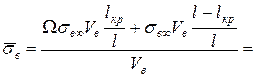
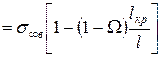 . (1.54)
. (1.54)
Якщо розтягуюча напруга від кінців волокон росте лінійно (мал. 13), то W = 0,5. Тоді середня напруга у волокнах
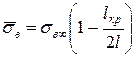 . (1.55)
. (1.55)
Відповідно до правила аддитивності загальна напруга, прикладена до КМ, рівна сумі середньої напруги в матриці і волокнах. Стосовно КМ з дискретними волокнами, що мають l> lкр, можна записати
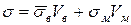 . (1.56)
. (1.56)
У момент руйнування 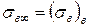 , а
, а 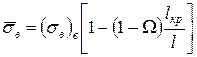 . Підставивши це значення замість
. Підставивши це значення замість 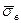 в рівняння (1.56) і замінивши в нім напругу в матриці sм напругою
в рівняння (1.56) і замінивши в нім напругу в матриці sм напругою 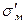 одержимо формулу для оцінки міцності КМ, армованою дискретними волокнами, яка разом з впливом об'ємної частки волокон враховує і вплив їх довжини:
одержимо формулу для оцінки міцності КМ, армованою дискретними волокнами, яка разом з впливом об'ємної частки волокон враховує і вплив їх довжини:
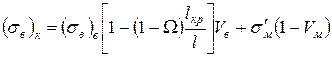 . (1.57)
. (1.57)
Як і при армуванні безперервними волокнами, межа міцності композиції з короткими волокнами росте пропорційно Vв, якщо Vв > Vmin. Із збільшенням відношення l/lкр міцність КМ зростає, наближаючись до міцності композицій з безперервними волокнами (l/ lкр = ¥).
Зіставивши між собою рівняння (1.41) і (1.57) і поклавши в останньому W»0,5, одержимо співвідношення між міцностями КМ, зміцнених дискретними і безперервними волокнами:
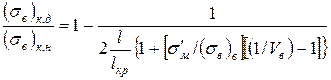 . (1.58)
. (1.58)
Як показують розрахунки, вже при l/lкр = 10 міцність КМ з дискретними волокнами досягає 95% міцності КМ з безперервними волокнами. Таким чином, армування дискретними волокнами дозволяє одержати практично ту ж міцність композицій, що і армування безперервними волокнами, якщо відрізки волокон достатньо довгі.
Мінімальну і критичну частку дискретних волокон в КМ розраховують так само, як і у разі КМ з безперервними волокнами. Наприклад
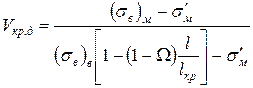 . (1.59)
. (1.59)
Критична і мінімальна частка дискретних волокон завжди більша, ніж відповідні значення для безперервних волокон. Наприклад, у алюмінію, армованого волокнами з (sв)в = 70 кгс/мм2, для безперервних волокон Vкр = 8,3%, а для дискретних волокон з l/lкр = 1 частка Vкp = 17,4%.
Дата добавления: 2016-07-27; просмотров: 1237;











