Нормальное распределение (распределение Гаусса).
Непрерывная случайная величина имеет нормальное распределение (распределена нормально или по Гауссу), если ее плотность имеет вид
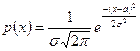 .
.
Вычислим математическое ожидание и дисперсию нормально распределенной случайной величины.
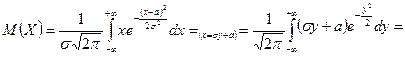
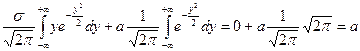 .
.
Вычислите аналогично 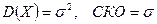 .
.
Обозначим плотность стандартного нормального распределения (при 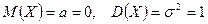 )
) 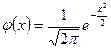 ,
,
обозначим функцию распределения стандартного нормального распределения
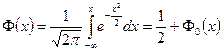 ,
,
где 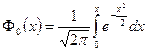 - интеграл Лапласа.Значения
- интеграл Лапласа.Значения 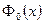 можно найти в стандартных таблицах.
можно найти в стандартных таблицах.
Вычислим вероятность попадания нормально распределенной случайной величины на отрезок [a,b].
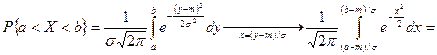
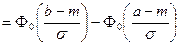 . При вычислении вероятности полезно учитывать нечетность функции
. При вычислении вероятности полезно учитывать нечетность функции 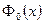 :
:
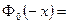
 .
.
Локальная и интегральная формулы Муавра – Лапласа.
Если в схеме Бернулли число испытаний n велико, причем p и q=1-p велики, то для всех m справедливы локальная формула Муавра – Лапласа
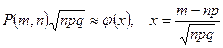 .
.
и интегральная формула Муавра – Лапласа
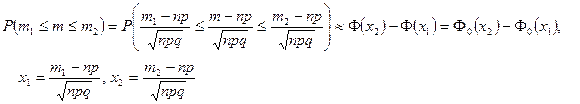 .
.
Это означает, что при большом числе испытаний распределение числа успехов становится нормальным.
Иногда приходится оценивать вероятность отклонения частоты события от вероятности. Покажем, как можно использовать для этого интегральную формулу Муавра – Лапласа.
Заметим, что 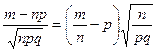 . Запишем интегральную формулу Муавра – Лапласа
. Запишем интегральную формулу Муавра – Лапласа
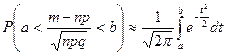 в виде
в виде
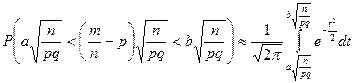 . Поэтому
. Поэтому
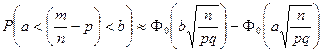 . Если интервал симметричен,
. Если интервал симметричен, 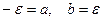 , то по нечетности
, то по нечетности 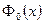
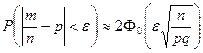 .
.
Примеры.
1) (3.42) Телефонная станция обслуживает 1000 абонентов. Вероятность вызова за минуту 0,0005. Какова вероятность, что за минуту поступит не менее двух вызовов? Здесь n = 1000, p = 0,0005, 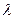 = np =0.5.
= np =0.5. 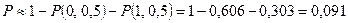 (по таблице
(по таблице 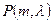 ).
).
2) (3.43) Известно, что 20% автомобилей нарушают скоростной режим. Какова вероятность того, что из 1000 автомобилей 210 нарушат правила? Здесь надо пользоваться локальной формулой Муавра-Лапласа при n=1000, p=0,2, m=300. 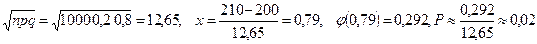
3) (3.44) Монету подбрасывают 10000 раз. Найти вероятность того, что частота выпадения герба будет отличаться от 0,5 не более, чем на 2%. Здесь надо пользоваться интегральной формулой Муавра-Лапласа при n=10000, р=1/2, m1=400, m2=600. Тогда 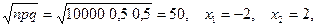
Дата добавления: 2016-07-27; просмотров: 2348;











