Свойства плотности.
1. 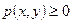 (функция распределения – неубывающая функция).
(функция распределения – неубывающая функция).
2. 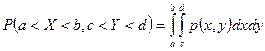 (по свойству 5 функции распределения) Справедливо обобщение
(по свойству 5 функции распределения) Справедливо обобщение 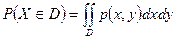 .
.
3. 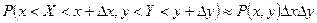
4. 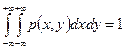 (по свойству 4 функции распределения)
(по свойству 4 функции распределения)
5. 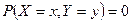
6. 
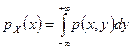 ,
, 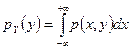 (Свойство 7 функции распределения)
(Свойство 7 функции распределения)
Независимость случайных величин.
Случайные величины X, Y называются независимыми, если 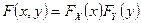 , где
, где 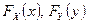 - функции распределения случайных величин X, Y.
- функции распределения случайных величин X, Y.
Если случайные величины непрерывны, то, дифференцируя это соотношение по x, y, получим 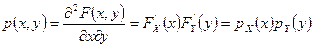 .
.
Соотношение 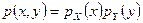 поэтому можно считать определением независимости непрерывных случайных величин.
поэтому можно считать определением независимости непрерывных случайных величин.
Длядискретныхслучайных величин определениенезависимостиможнозаписать в виде 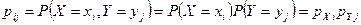 .
.
Математическое ожидание.
Математическим ожиданием функции двумерной случайной величины называется
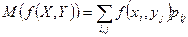 в дискретном случае,
в дискретном случае,
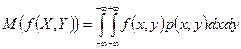 в непрерывном случае.
в непрерывном случае.
Свойства математического ожидания
1. 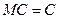 (
(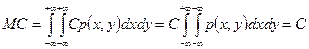 по условию нормировки)
по условию нормировки)
2. 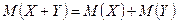
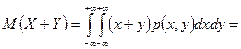
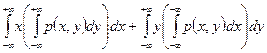 =
= 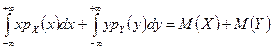
3 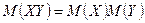 для независимыхслучайных величин.
для независимыхслучайных величин.
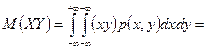
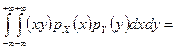
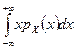
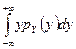 =
= 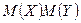 .
.
Ковариация (корреляционный момент).
Ковариацией случайных величин называют 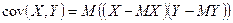 .
.
Дата добавления: 2016-07-27; просмотров: 1757;











