Повторные испытания.
Пусть производится n опытов (испытаний), в каждом из которых может наступить один из N исходов. Если результаты одного испытания не зависят от результатов других испытаний, то такие испытания называются независимыми.
Например, стрелок делает n выстрелов в мишень, в которой N колец: десятка, девятка и т.д.
Возможны две ситуации: условия проведения испытаний не меняются (ситуация А) или меняются от испытания к испытанию (ситуация В).
Рассмотрим ситуацию А.
Пусть число исходов равно двум (N = 2). Схема независимых испытаний с двумя исходами называется схемой Бернулли.
Два исхода соответствуют в приведенном примере попаданию (успеху) или не попаданию в мишень, причем в каждом выстреле вероятность попадания равна p, а вероятность промаха равна q = 1 – p. Обозначим вероятность попасть m раз из n выстрелов P(m,n). 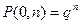 , так как в каждом опыте стрелок промахивается. Вероятность попасть один раз равна
, так как в каждом опыте стрелок промахивается. Вероятность попасть один раз равна 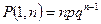 , так как стрелок может попасть при первом, втором, … n ом выстреле.
, так как стрелок может попасть при первом, втором, … n ом выстреле. 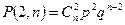 ,так как два попадания (порядок не важен) должны быть размещены (выборки без возвращения) среди n выстрелов. Аналогично
,так как два попадания (порядок не важен) должны быть размещены (выборки без возвращения) среди n выстрелов. Аналогично
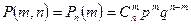 - формула Бернулли.
- формула Бернулли.
Само распределение 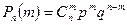 называют биномиальным.
называют биномиальным.
В самом деле, это – коэффициенты при 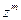 в разложении по степеням
в разложении по степеням 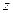
производящей функции 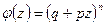 .
.
Из формулы Бернулли вытекают два следствия:
1) Вероятность появления успеха в n испытаниях не более m1 раз и не менее m2 раз равна 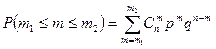 ,
,
2) Вероятность хотя бы одного успеха в n испытаниях равна 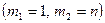
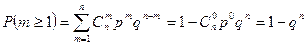 .
.
Если Х имеет биномиальное распределение, то Мх = np, Dx = npq.
Пусть в ситуации А число исходов равно N, а их вероятности равны p1…pN . Вычислим вероятность того, что после n испытаний i – тый исход наступит 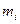 раз
раз 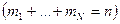
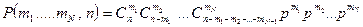 .
.
Заметим, что 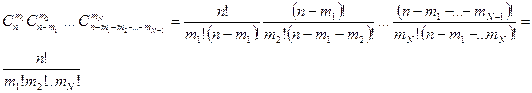 .
.
так как 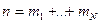 .
.
Поэтому 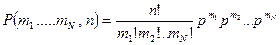 . Это – полиномиальное распределение.
. Это – полиномиальное распределение.
Заметим, что 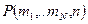 - это коэффициенты при
- это коэффициенты при 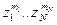 в разложении по степеням
в разложении по степеням 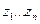 производящей функции
производящей функции 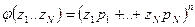 .
.
Рассмотрим ситуацию В. Здесь вероятность того или иного исхода зависит от номера испытания, так как условия испытаний различны. 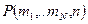 - это коэффициенты при
- это коэффициенты при 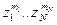 в разложении по степеням
в разложении по степеням 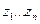 производящей функции
производящей функции 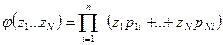 при N исходах.
при N исходах.
При двух исходах 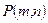 - это коэффициент при
- это коэффициент при 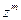 в разложении производящей функции
в разложении производящей функции
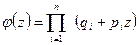 , где
, где 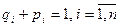 .
.
Примеры.
1) Какова вероятность с пяти раз вытащить из колоды в 36 карт а)три туза, б)не менее одного туза?
а) 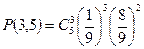 , б)
, б) 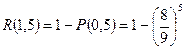 .
.
2) Мишень для опытного стрелка содержит три круговых кольца: 10, 9, пусто. Вероятность попасть при одном выстреле в десятку – 0,2, в девятку – 0,7, в «пусто» – 0,1. Какова вероятность в серии из 10 выстрелов попасть в «пусто» два раза, в девятку 4 раза, в десятку 4 раза?
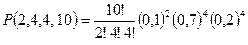
3) Производится три выстрела в мишень. При первом выстреле вероятность попасть в мишень равна 0,5, не попасть 0.5. При втором выстреле – соответственно 0,4 и 0.6, при третьем выстреле 0,3 и 0,7. Какова вероятность два раза попасть в мишень?
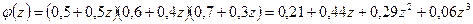 .
.
Вероятность не попасть ни разу 0,21, один раз – 0,44, два раза – 0,29, три раза – 0,06.
Дата добавления: 2016-07-27; просмотров: 1806;











