Свойства ковариации.
1. 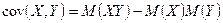
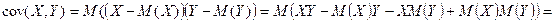
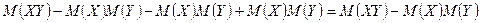
2. 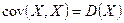
По свойству 1 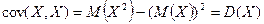
3.Если X, Y независимы, то 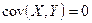 , (обратное неверно).
, (обратное неверно).
Если случайные величины независимы, то 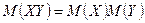 , тогда по свойству 1
, тогда по свойству 1 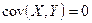 .
.
Случайные величины называются некоррелированными, если 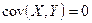 , из некоррелированности не следует независимость, из независимости следует некоррелированность.
, из некоррелированности не следует независимость, из независимости следует некоррелированность.
Коэффициентом корреляциислучайных величин X и Y.называется 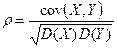 .
.
Можно показать, что 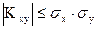 , поэтому
, поэтому 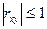 . Если
. Если 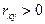 , то говорят, что между X и Y существует положительная корреляция; это означает, что с увеличением значений одной случайной величины, другая имеет тенденцию к возрастанию. Если
, то говорят, что между X и Y существует положительная корреляция; это означает, что с увеличением значений одной случайной величины, другая имеет тенденцию к возрастанию. Если 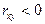 , то говорят, что между X и Y существует отрицательная корреляция; это означает, что с увеличением значений одной случайной величины другая имеет тенденцию к убыванию. Если
, то говорят, что между X и Y существует отрицательная корреляция; это означает, что с увеличением значений одной случайной величины другая имеет тенденцию к убыванию. Если 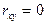 , это означает, что случайные величины X и Y некоррелированны.
, это означает, что случайные величины X и Y некоррелированны.
Если между случайными величинами X и Y существует линейная зависимость, то 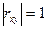 . Действительно, пусть
. Действительно, пусть 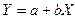 . В этом случае
. В этом случае
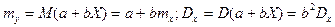 ;
;
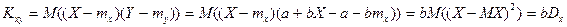 .
.
Тогда
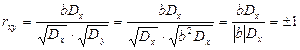 .
.
Информацию о связи между компонентами X и Y системы (X,Y) несет корреляционная матрица , которая имеет вид
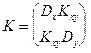 .
.
Матрица К является симметричной вследствие равенства 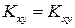 .
.
Кроме корреляционного момента и коэффициента корреляции , взаимная связь двух случайных величин может быть описана с помощью линий регрессии.
Действительно, при каждом значении Х = х величина Y остается случайной величиной, допускающей рассеяние своих значений, однако зависимость Y от Х сказывается также в изменении средних значений Y при переходе от одного значения X к другому. Эту зависимость и описывает кривая регрессии
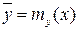 .
.
Аналогично, зависимость X от Y, которая сказывается в изменении средних значений X при переходе от одного значения Y = y к другому, описывается кривой регрессии
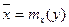 .
.
Наиболее простым случаем будет тот, когда обе функции линейны, так что обе линии регрессии будут прямыми линиями; они называются прямыми регрессии. В этом случае будем говорить о линейной корреляции между случайными величинами X и Y.
Выведем уравнения прямых регрессии. Пусть MX = mx, MY = my, Dx = 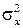 , Dy =
, Dy = 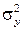 , Kxy – корреляционный момент случайных величин X и Y. Будем искать уравнение прямой регрессии Y на X в виде
, Kxy – корреляционный момент случайных величин X и Y. Будем искать уравнение прямой регрессии Y на X в виде 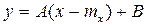 , где параметры A и B подлежат определению.
, где параметры A и B подлежат определению.
Взяв математическое ожидание от обеих частей последнего равенства и учитывая, что 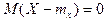 , имеем, что
, имеем, что 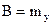 . Далее
. Далее
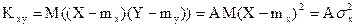 , откуда
, откуда 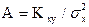 .
.
Таким образом, в случае линейной корреляции уравнение прямой регрессии Y на X имеет вид
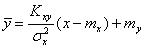 .
.
Аналогично уравнение прямой регрессии X на Y имеет вид
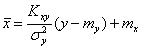 .
.
Если учесть, что 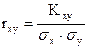 , то уравнения прямых регрессии могут быть переписаны в симметричной форме:
, то уравнения прямых регрессии могут быть переписаны в симметричной форме:
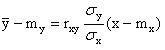 ;
;
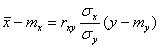 .
.
Из уравнений прямых регрессии (3.3.13) и (3.3.14) видно, что обе прямые проходят через точку (mx,my). Угловые коэффициенты прямых регрессии равны соответственно:
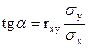 ,
, 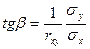 .
.
Так как 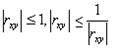 , прямая регрессии Y на X имеет меньший угол наклона к оси Ох, чем прямая регрессии X на Y. Чем ближе
, прямая регрессии Y на X имеет меньший угол наклона к оси Ох, чем прямая регрессии X на Y. Чем ближе 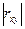 к 1, тем меньше угол между этими прямыми; при
к 1, тем меньше угол между этими прямыми; при 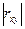 = 1 прямые регрессии сливаются. При
= 1 прямые регрессии сливаются. При 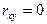 прямые регрессии имеют уравнения
прямые регрессии имеют уравнения 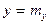 и
и 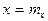 , так что обе они параллельны соответствующим осям координат. В этом случае величины X и Y являются некоррелируемыми; для них
, так что обе они параллельны соответствующим осям координат. В этом случае величины X и Y являются некоррелируемыми; для них 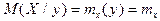 ,
, 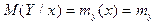 , т. е. условные математические ожидания совпадают с безусловными.
, т. е. условные математические ожидания совпадают с безусловными.
Дата добавления: 2016-07-27; просмотров: 3581;











