Свойства дисперсии.
1) 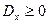 (под интегралом стоит квадрат функции).
(под интегралом стоит квадрат функции).
2) 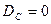 (
( 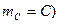 .
.
3) 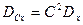 (выведите сами, вынося
(выведите сами, вынося 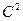 из под суммы или из под интеграла).
из под суммы или из под интеграла).
Средним квадратическим отклонением называется 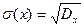 .
.
Кроме этих основных числовых характеристик используются коэффициент асимметрии 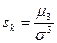 , эксцесс – мера островершинности распределения
, эксцесс – мера островершинности распределения 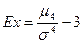 , среднее арифметическое отклонение
, среднее арифметическое отклонение 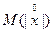 , мода – наиболее вероятное значение для дискретных величин или значение, где плотность максимальна для непрерывных величин, медиана Me – абсцисса точки, в которой площадь, ограниченная кривой плотности распределения, делится пополам (точка, в которой F(x) = ½).
, мода – наиболее вероятное значение для дискретных величин или значение, где плотность максимальна для непрерывных величин, медиана Me – абсцисса точки, в которой площадь, ограниченная кривой плотности распределения, делится пополам (точка, в которой F(x) = ½).
Пример.Стрелок делает один выстрел и с вероятностью p попадает в мишень. Пусть X – количество попаданий в мишень. Это – дискретная случайная величина, принимающая два значения х1 = 0 и х2 = 1 с вероятностями q = 1-p, p соответственно. Построим ряд распределения Х
| xi | ||
| pi | q | p |
Функция распределения равна 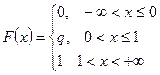 ,
,
Математическое ожидание равно M(X) = mx = 0 q + 1 p = p.
Если составить ряд распределения для случайной величины X2, то мы получим ту же таблицу (так как 02 = 0 и 12 =1). Поэтому M(X2) = p, а дисперсию можно вычислить по формуле D(X) = M(X2) – (mx)2 = p – p2 = p(1-p) = pq.
Распределение называется равномерным на отрезке [a,b],еслиплотность случайной величины X постоянна на отрезке [a,b] p(x) = p и равна нулю вне этого отрезка.
Из условия нормировки для плотности вероятности следует
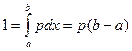 . Отсюда следует, что
. Отсюда следует, что 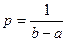 - плотность равномерного распределения. Функция распределения величины, распределенной равномерно на отрезке [a,b], равна
- плотность равномерного распределения. Функция распределения величины, распределенной равномерно на отрезке [a,b], равна
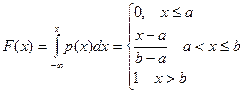 . Вычислим математическое ожидание и дисперсию величины, распределенной равномерно на отрезке [a,b].
. Вычислим математическое ожидание и дисперсию величины, распределенной равномерно на отрезке [a,b].
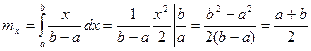 ,
,
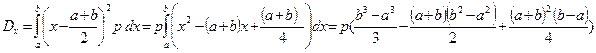 =
= 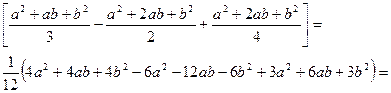
= 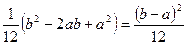
Дата добавления: 2016-07-27; просмотров: 1675;











