Общие понятия об интерполировании.

Рассмотрим следующую задачу. Пусть функция f(x) задана таблично, т. е.

известны её значения в (n+1) – точках x_i Є[a,в], где i=0,1,2…n f(x_i) =y_i

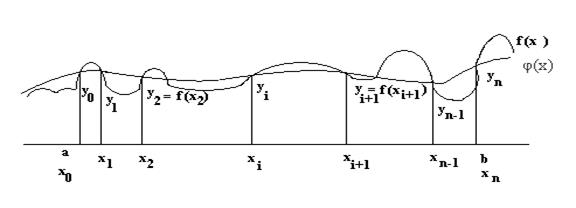
Точки x₀x₁x₂…x_n называются узлами интерполяции. Требуется найти простую функцию φ(х), что φ(x_i)= f(x_i) в узлах интерполяции и φ(x)≈ f(x) в остальных точках х.

Пусть 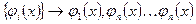-последовательность вещественных функций. Тогда 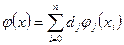называется обобщенным полиномом.

Обобщенный полином называют интерполяционным, если f(x_i)= φ(x_i) i=0,1,2… в узлах интерполяции. Обычно в качестве {φ_i(x)} берутся функции.

1) 1, х, х², х³…

2) 1, sinx, cosx, sin2x, cos2x…

3) 1, e^λ1х, e^λ2х, e^λ3х…

λ₁ λ₂ …λ_n- некоторая последовательность.

Линейная интерполяция.

При линейной интерполяции предполагается, что функция f(x) между узлами интерполяции изменяется по линейному закону (см. рис)

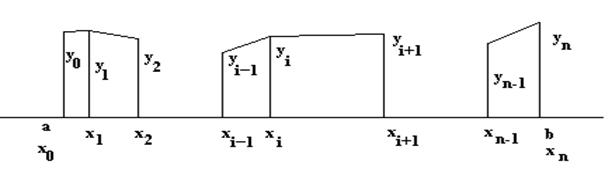
из геометрии уравнение прямой, проходящей через точки (x_i-1 y_i-1) и (x_i y_i) будет иметь вид (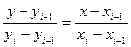

Отсюда для каждого x, лежащего в интервале [x_i-1 x_i ] может быть найдено соответствующее значение y по формуле

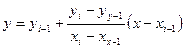
Таким образом, мы можем найти любое f(x) =y на любом отрезке интерполяции.