Метод половинного деления (бисекций).

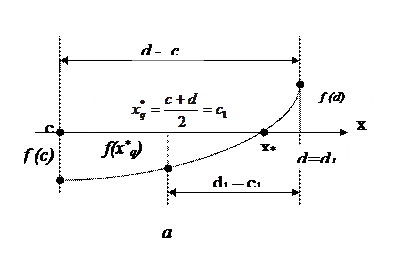
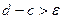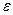Пусть простой корень х_* уравнения f(x)=0 определён и находится на отрезке [c, d], т.е. f(c)f(d)<0, причём , где - допустимая погрешность вычисления. Возьмём в середине [c, d] точку 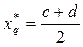. Очевидно, что при 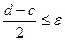точка х^*_q будет искомым корнем уравнения. В противном случае сделаем первый шаг к уточнению корня.

Вычислим 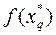. Если 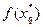=0, то корень уравнения 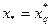. Если 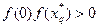(рис. а), то х_* лежит внутри интервала 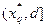, который обозначим как 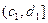. Если 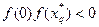, то х₀ лежит в нутрии 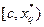, который обозначим как 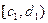(рис. б). В обоих случаях длинна отрезк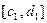а равна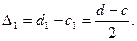

Возьмём в середине отрезка 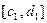точку 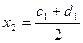. Тогда при 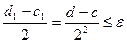точка х₂ будет значением корня в заданной погрешностью. В противном случае, аналогично, сделаем второй шаг. При этом получим новый отрезок 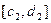длиной 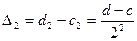и т.д. На каком то шаге точка 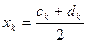будет корнем уравнения с заданным приближением 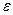при выполнении неравенства 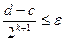. Из последнего можно определить число шагов, обеспечивающих достижения требуемой точности вычислений:

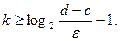
Изложенный метод, называемый методом половинного деления (метод бисекций), сходится для любых непрерывных функций, в том числе и для недифференциальных.

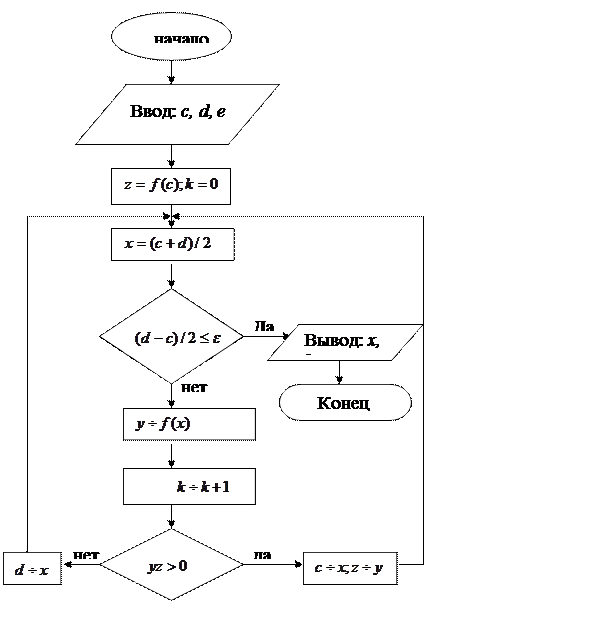
Блок схема алгоритма метода бисекций:

Метод итераций.

Приведём уравнение 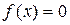к виду 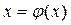(1)

Возьмём некоторую произвольную точку 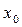на оси 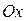. Если существует такая точка 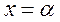, что 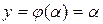, то очевидно, число 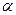и будет корнем уравнения (1). В общем случае 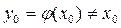. Суть метода простых итераций (повторений) состоит в построении последовательности { 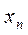} точек, сходящихся к корню 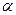, где , (2)

При этом 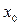называют начальным приближением.

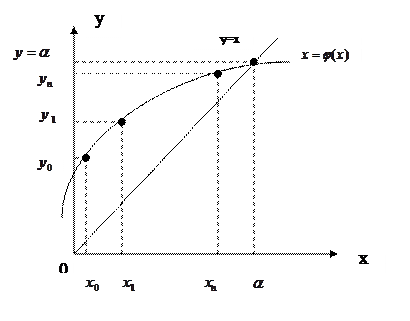
Необходимо отметить, что последовательность { 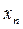} не всегда является сходящейся. Рассмотрим пример:

Линейное уравнение 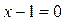, имеющее корень 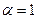можно преобразовать к виду 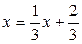или .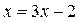

Взяв за начальное приближение 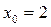, в первом случае получим

; , …

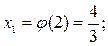
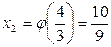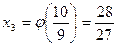Данная последовательность стремится к точному решению уравнения.

Во втором случае

; ; , …

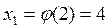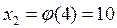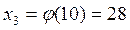Эта последовательность расходится.

Следовательно, вид функции 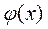оказывает существенное влияние на сходимость итерационного процесса.

Сходимость метода простой итерации определяется следующей теоремой: При любом начальном приближении 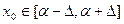на некотором интервале последовательность 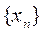, построенная в соответствии с методом простой итерации (2), сходится к корню 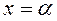, который является единственным решением уравнения (1) на рассматриваемом интервале, если здесь функция 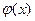удовлетворяет условию Липшица

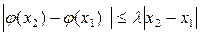
с постоянной Липшица .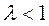

Если функция 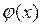дифференцируема и имеет на 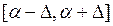ограниченную производную, то постоянная Липшица .

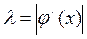В рассмотренных выше примерах для уравнения 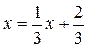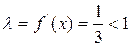и итерационный процесс является сходящимся к корням уравнения .

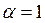Для уравнения 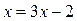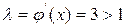и условия сходимости не выполняется.

Если вычисление постоянной Липшица сопряжено с определёнными математическими трудностями, то алгоритм метода простой итерации использует косвенную оценку точности вычислений

,

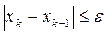где 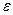- допустимая погрешность вычислений.

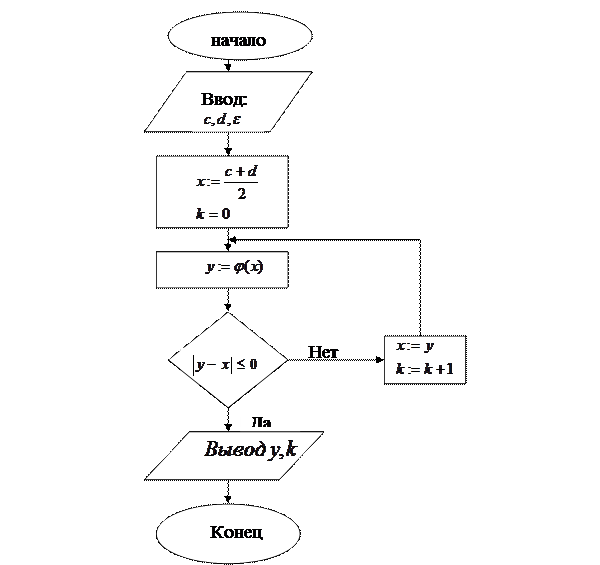
Блок – схема алгоритма метода простой итерации с косвенной оценкой точности вычислений:

Лекция 7