Интерполяционный полином Ньютона для неравно отстоящих значений аргумента
Пусть f(x) ¾ некоторая функция, а x0,x1,…xn ¾ узлы интерполяции, а x ¾ произвольная, но фиксированная точка значения аргумента. Тогда имеем:
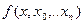 =
= 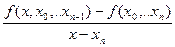
Откуда:
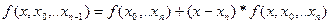
Аналогично:
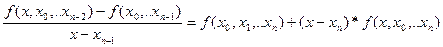
Откуда
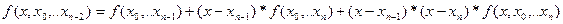
продолжая этот процесс далее, получим:
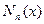
 |
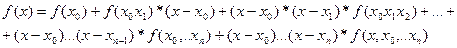
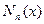
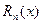
Эта форма записи носит название интерполяционной многочлена Ньютона для неравных промежутков или
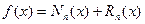
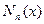 ¾полином n-степени,
¾полином n-степени, 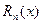 ¾остаточный член.
¾остаточный член.
 | |||
 |
Можно показать, что полином Ньютона и полином Лагранжа совпадают Nn(x)= Ln(x), т.е. равный их остаточный член.
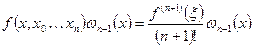
Или
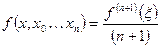
Полином Ньютона удобнее полинома Лагранжа тем, что при добавлении новых узлов интерполяции все проведенные вычисления в полиноме Ньютона сохраняются, а в полиноме Лагранжа нет.
Конечные разности.
В случаях когда узлы интерполяции берутся равноотстоящими
xk=x0+k*h k=0,1,2…n
n- шаг интерполирования, то часто вводят следующие обозначения
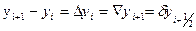 – конечные разности
– конечные разности
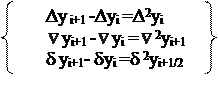 |
0нисходящие
восходящие - конечная разность 2го порядка
центральные
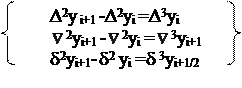
- конечная разность 3го порядка
Связь конечных разностей и разделенных разностей.
Для равностоящих значений аргумента xk=x0+k*h имеем:
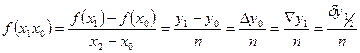
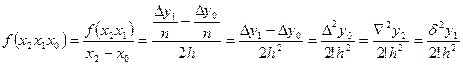
_ _ _ _ _ _ _ _ _ _
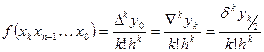
Дата добавления: 2016-07-27; просмотров: 2008;











