Интерполяционный многочлен Лагранжа.

Точность аппроксимации можно повысить, если вместо линейной функции использовать алгебраический многочлен

L_n(x)= a₀+ a₁x+a₂x²+…+ a_nxⁿ

Будем искать его в виде.

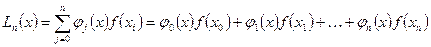(1)

где φ_j (x) – многочлен n, который удовлетворяет условия

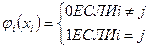
В n точках полином обращается в нуль и только в одной точке i=j обращается в 1. Раз он обращается в нуль в n точках, то в нем должен быть множитель

φ_j (x)=С_j (x-x₀ )(x-x₁ )…(x-x_j-1 )(x-x_j+1 )… (x-x_n ) (2)

где С_j – неопределенный коэффициент.

Надо потребовать, чтобы в точке i=j он обратился в 1

1=φ_j (x_j)=С_j (x-x₀)(x-x₁ )…(x-x_j-1 )(x-x_j+1 )…(x-x_n )

и тогда

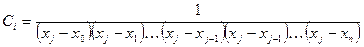(3)

Или подставляя (3)→(2) получим

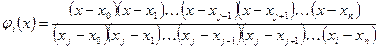(4)

Подставляя (4) в (1) получим

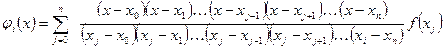(5)

L_j ⁽ⁿ⁾(x)

Полученный полином называют интерполяционным полиномом Лагранжа.

Если ввести обозначение ω_n+1(x)= (x-x₀)(x-x₁₎… (x-x_n ), то полином Лагранжа заменяется в виде:

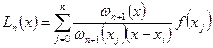(6)

L_j ⁽ⁿ⁾(x)

Тогда φ_j (x) и L_j ⁽ⁿ⁾(x) называются Лагранжевыми коэффициентами. Составление полинома Лагранжа и вычисление его в отдельных точках в ручную довольно таки трудоемкая задача. Добавление лишнего узла приводит к пересчету всех коэффициентов. Остаточный член интерполяционной формулы Лагранжа выглядит так

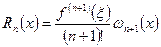(7)

Тогда

f(x)= L_n(x)+ R_n(x)