Классификация уравнений. Этапы численного решения.

Любое уравнение может быть записано в следующем общем виде

f(x)=0.

Если f(x) – алгебраическая функция (например, f(x)=x⁴+2x-1, f(x)= 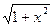), то уравнение называют алгебраическим. Всякое алгебраическое уравнение может быть преобразовано к виду

a₀ xⁿ + a₁ x^n-1 +…+ a_n-1x + a_n=0. (*)

Если f(x) не является алгебраической (содержит степенную, логарифмическую, функцию sin, cos и т.д.), то уравнение называют трансцендентным (например, f(x)=2^x + lnx - 6) .

Решить уравнение – это значит найти такие значения x, (которые называют корнями уравнения), при которых заданные уравнения обращается в тождество.

При численном приближённом решением уравнения выделяю 2 этапа:

1. отделение корней – отыскание достаточно малых интервалов, в каждом из которых один и только один корень уравнения;

2. вычисление каждого корня с заданной точностью внутри выделенного интервала.

Отделение корней.

Пусть [a, b] – интервал изменения х, в котором отыскиваются вещественные корни уравнения f(x)=0, где f(x) – непрерывная функция вещественного переменного. Разбив [a, b ] на n отрезков длинной 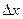, наличие простого корня 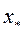в интервале [x_k-1, x_k], k=1, 2, … , n, легко установить по знаку произведения концевых значений функции f:

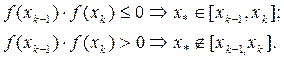
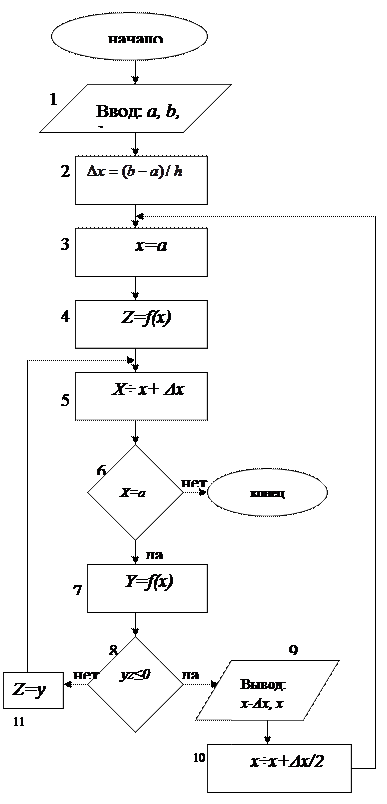
Алгоритм определения корней можно показать следующей блок схемой (см. лист 9). Алгоритм предусматривает ввод (блок 1) исходных данных (a, b – начало и конец исследуемого интервала, n – число одинаковых отрезков разбития [a, b] на подынтервалы) и определение величины 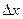(блок 2). Далее для каждого интервала 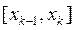длиной 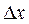вычисляется 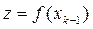(блок 3) и y=f(x_k) (блок 7), а затем, в результате исследования знака произведения 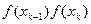(блок 8), решается вопрос о существовании на 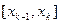простого корня. При 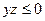предусматривается выдача значений границ 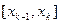(блок 9) и выявление начала следующего интервала (блок 10).

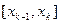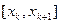Если отказаться от блока 10, то при случайном совпадении корня с точкой x_k деление отрезка произойдёт выдача на печать значений двух интервалов и , хотя нам достаточно одного.

При определении корней алгебраического уравнения (*) можно воспользоваться следующими закономерностями:

а) алгебраические уравнения п – го порядка имеет п корней, среди которых могут быть вещественные и комплексные;

b) число положительных вещественных корней равно числу (или меньше на чётное число) перемен законов в последовательности коэффициентов a₀, a₁ , a₂ , … , a_n , причём равные нулю коэффициенты не учитываются (теорема Декарта).

После отделения корней можно приступать к нахождению корня с заданной точностью на каждом выделенном интервале.