Распределение джонсона

Г. Г. Сванидзе и Г. Л. Григолия рекомендуют использовать для анализа колебаний речного стока кривые распределения Джонсона [49, 64б]. Джонсон предложил находить эмпирическое распределение пу­тем нормализации распределения случайной величины..

В общем случае преобразование Джонсона имеет вид [49]

δ>0, -∞<ν<∞,

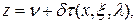(4.91)

λ>0, -∞<ξ<∞,

где X — случайная величина, для которой подбирается кривая Джонсона; τ—некоторая произвольная функция; v, δ, ξ, λ — па­раметры распределения; z —нормированная случайная величина, подчиняющаяся нормальному закону распределения.

Исходя из вида функции τ(х, ξ, λ.) Джонсоном предложены три различные формы, или семейство функций:

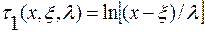, x≥ξ; (4.92)

, ξ≤x<ξ+λ (4.93)

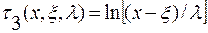, -∞<x<∞ (4.94)

Распределение, основанное на преобразовании τ₁, представляет собой логарифмически нормальное распределение с тремя пара­метрами, называемое семейством распределения S_L Джонсона; распределение, основанное на преобразовании τ₂, представляется в виде семейства распределения S_B Джонсона с четырьмя пара­метрами распределения; а τ ₃ — семейство распределений S_v Джон­сона также с четырьмя параметрами распределения. Как следует из приведенных формул, распределения S_L., S_B, S_v применяются соответственно для случайных величин, ограниченных с одной сто­роны (I тип), случайных величин, ограниченных сверху и снизу (II тип) и, наконец, для неограниченных случайных величин.

При исследовании геоэкологических процессов наибольший инте­рес представляет ограниченное с двух сторон распределение S_B (II тип).

Плотность распределения S_B Джонсона можно записать в сле­дующем виде:

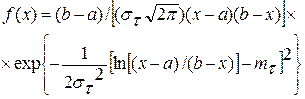(4.95)

где b=λ+ξ и а = ξ, — верхняя и нижняя граница случайной вели­чины X; т_τ и σ_τ—математическое ожидание и среднее квадратическое отклонение Т.

Отдельные значения Т с учетом введенных обозначений нижней и верхней границы [см. формулу (4.92)] рассчитываются по формуле

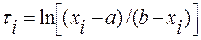, (4.96)

где i — порядковый номер члена ряда X и Т (i= 1, 2, .. ., N) (ин­декс, обозначающий номер семейства функций, в дальнейшем опускается, так как рассматривается только семейство S_b).

Числовые характеристики Т — m_τ и σ_τ вычисляются по формулам:

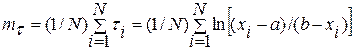; (4.97)

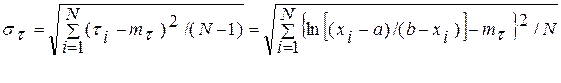(4.98)

Расчеты ординат кривой Джонсона обычно проводятся по нор­мированным ординатам (3.35)

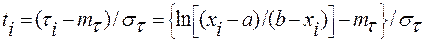. (4.99)

t_i в этом случае, так же как и τ_i, подчиняется нормальному закону распределения и, кроме того, m_t = 0, σ_t =1.

При построении кривой обеспеченности Джонсона возможны следующие ситуации:

параметры а и b известны,

известен пара­метр а или b,

ни одно из крайних значений неизвестно.

В первом случае по ряду X рассчитывается последовательность значений τ [см. формулу (4.96)] и числовые характеристики этой последовательности m_τ и σ_τ[см. формулы (4.97) и (4.98)]. Затем из таблицы нормированных ординат нормального закона распре­деления для заданных значений обеспеченности берутся значения нормированных ординат t_Р. По известным значениям t_P определя­ются [см. формулу (4.99)] значения

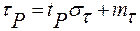(4.100)

и на основе формулы (4.95) значения ряда X обеспеченностью Р%

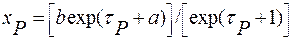; (4.101)

Во втором случае, когда известно одно из крайних значений, в качестве которого чаще всего выступает параметр а — нижняя граница значения X, на первом этапе подбором определяется па­раметр b. В качестве критерия подбора (критерий качества) обычно принимается какой-либо количественный показатель со­гласия (совпадения) кривой обеспеченности Джонсона с эмпири­ческими точками. В качестве такого критерия обычно принима­ется критерий согласия Пирсона (χ²). Нам представляется более целесообразным использование критерия nω². (Описание крите­риев согласия дано в главе 6.)

Таким образом, процедура расчетов заключается в следующей последовательности действий; при известном значении а (или b) .задаем какое либо значение b=b₁. В качестве b₁ может выступать, например, максимальное наблюденное значение X — х_макс. Для значения а и b₁ по изложенной для первого случая схеме рассчи­тываются значения координат теоретической кривой обеспеченно­сти и определяется критерий χ₁² или nω₁. Затем задаем новое значение b = b₂, b₂> b₁, снова рассчитываем координаты теоретической кривой и находим χ ₂² и nω₂²и т. д. По данным расчетов стро­ится график зависимости χ₂= f(b) или nω₂² =f(b) или просто про­изводится сравнение значений этих критериев. В качестве расчет­ного выбирается то значение b, при котором значения χ²или nω²являются наименьшими, т. е. отклонение эмпирических точек от теоретической кривой является наименьшим.

В качестве примера на рис. 4.7 представлен график зависимо­сти nω² = f(b) для минимального стока р. Иртыш, для которого можно принять а=0.

В третьем случае, когда неизвестны оба предела колебаний X, производится подбор параметров а и b. В этом случае назнача­ется какое-то малое предельно возможное а, или в качестве а принимается х_мин. Затем, также как во втором случае, подбира­ется параметр b. Затем назначается новое значение а и снова вы­полняется подбор b и т. д. На основе расчетов строится график χ² = f(a, b) или nω² = f(a, b) и выбираются такие значения а и b, при которых названные критерии являются минимальными (рис. 4.7).

Рис. 4.6. Изменение критерия согласия ηω² в зависимости от нижнего (а) и верхнего (б) предела распределения S_в Джонсона.