T – распределение Стьюдента

Закон нормального распределения проявляется при числе признаков n > 20–30. Однако экспериментатор часто проводит ограниченное число измерений, основывает свои выводы на малых выборках. При небольшом числе наблюдений результаты обычно близки и редко появляются большие отклонения. Это легко объяснить законом нормального распределения, согласно которому вероятность появления малых отклонений больше, чем отклонений значительных. Так, вероятность отклонений, превышающих по абсолютной величине ±2σ, равна 0,05, или один случай на 20 измерений, а отклонений ± 3σ – 0,01, или один случай на 100.

Если же полевой опыт проводят, например, в 4 – 6 повторностях, то естественно ожидать, что среди показаний урожаев на параллельных делянках очень больших отклонений не будет. Поэтому стандартное отклонение s, подсчитанное по малой выборке, в большинстве случаев будет меньше, чем по всей генеральной совокупности . Следовательно, в этих случаях полагаться на критерии нормального распределения в своих выводах нельзя.

С начала XX века в математической статистике стало разрабатываться новое направление, которое можно назвать статистикой малых выборок. Наибольшее практическое значение для экспериментальной работы имело открытое в 1908 г. английским статистиком и химиком В. Госсетом t–распределение, получившее название распределения Стьюдента (англ. стьюдент – студент, псевдоним В. Госсета).

Распределение t Стьюдента для выборочных средних определяется равенством:

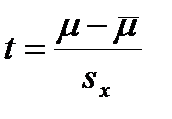(5.1)

Числитель формулы означает отклонение выборочной средней от средней всей совокупности 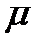, а знаменатель:

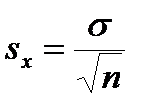– является показателем, оценивающим величину стандартной ошибки средней выборочной совокупности.

Таким образом, величина t измеряется отклонением выборочной средней 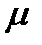от средней совокупности 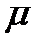, выраженным в долях ошибки выборки 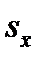, принятой за единицу.

Максимумы частоты нормального и t-распределения совпадают, но форма кривой t-распределения всецело зависит от числа степеней свободы. При очень малых значениях степеней свободы она принимает вид плосковершинной кривой, причем площадь, отграниченная кривой, больше, чем при нормальном распределении, а при увеличении числа наблюдений (n > 30) распределение t приближается к нормальному и переходит в него при n = ∞.

На рисунке 1.1 представлено дифференциальное и интегральное распределение t-Стьюдента при 10 степенях свободы.

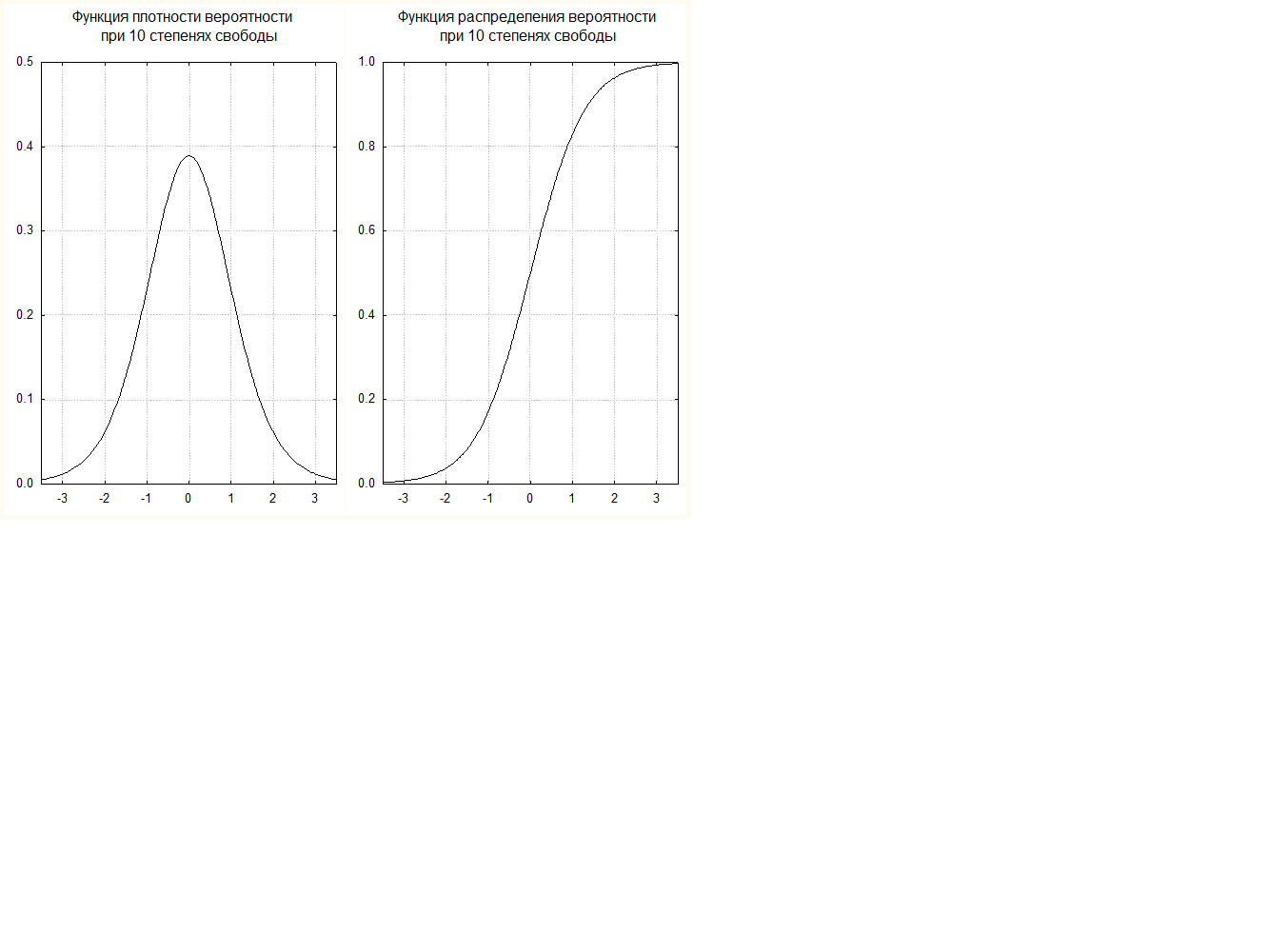
Рисунок 5.1 – Дифференциальное (слева) и интегральное (справа) распределение t–Стьюдента

Распределение t–Стьюдента имеет важное значение при работе с малыми выборками: позволяет определить доверительный интервал, накрывающий среднюю совокупности 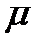, и проверить ту или иную гипотезу относительно генеральной совокупности. При этом нет необходимости знать параметры совокупност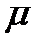и и , достаточно иметь их оценки μ и σ для определенного объема выборки n.