F-распределение Фишера–Снедекора

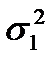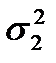Если из нормально распределенной совокупности взять две независимые выборки объемом n₁ и n₂ и подсчитать дисперсии и со степенями свободы ν₁ = n –1 и ν₂ = n₂–1, то можно определить отношение дисперсий:

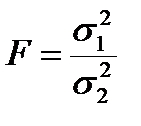(5.2)

Отношение дисперсий берут таким, чтобы в числителе была большая дисперсия, и поэтому F ≥ 1.

Распределение F зависит только от числа степеней свободы ν₁ и ν₂ (закон F-распределения открыл Р.А. Фи шер). Когда две сравниваемые выборки являются случайными независимыми из общей совокупности с генеральной средней 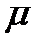, то фактическое значение F не выйдет за определенные пределы и не превысит критическое для данных ν₁ и ν₂ теоретическое значение критерия F (F_факт < F_теор). Если генеральные параметры сравниваемых групп различны, то F_факт > F_теор. Теоретические значения F для 5%-ного и 1%-ного уровня значимости даны в таблице, где табулированы только правые критические точки для F ≥ 1, так как всегда принято находить отношение большей дисперсии к меньшей.

Кривые, полученные из функции распределения для всех возможных значений F, особенно при небольшом числе наблюдений, имеют асимметричную форму – длинный «хвост» больших значений и большую концентрацию малых величин F (рисунок 5.2).

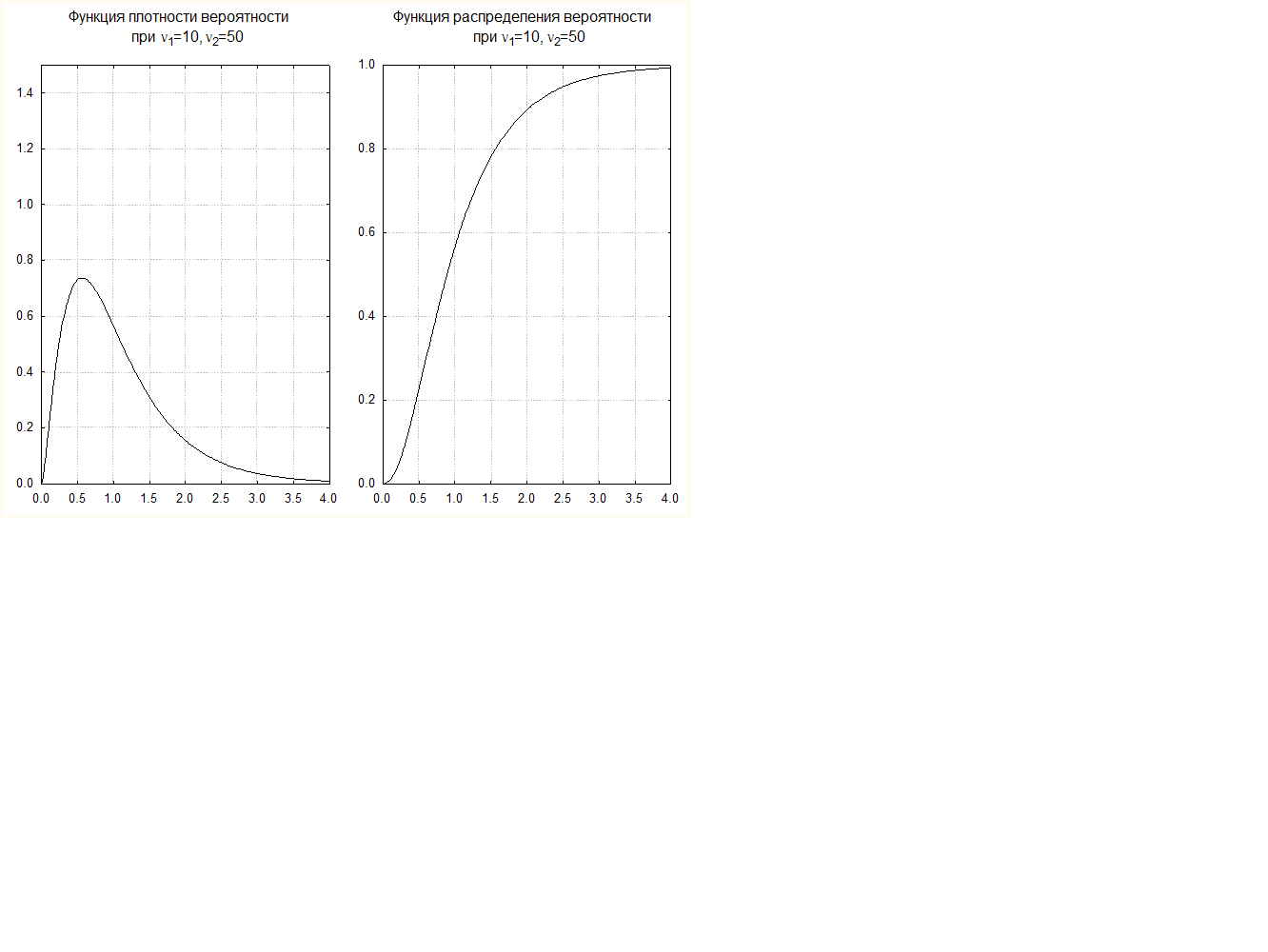
Рисунок 5.2 – Дифференциальное (слева) и интегральное (справа)
F-распределение Фишера–Снедекора

Отметим, что t–распределение Стьюдента является частным случаем F–распределения при числе степеней свободы ν₁ = 1 и ν₂ = ν, т. е. равно числу степеней свободы для распределения t. В этом случае наблюдается следующее соотношение между F и t:

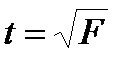(5.3)

5.3 χ²–распределение

Многие фактические распределения соответствуют моделям теоретических распределений (нормальное, биномиальное, Пуассона) Однако, на практике существуют распределения, сильно отличающиеся от нормального. Для оценки степени расхождения или степени согласия между численностями фактического и теоретического распределений вводятся статистические критерии согласия, например критерий χ² . Этот критерий применяется для решения задач статистического анализа, например для проверки гипотез: о независимости двух принципов, положенных в основу группировки результатов наблюдений из одной совокупности; об однородности групп в отношении некоторых определяемых характеристик; о согласии теоретической и экспериментальной кривых численностей. Критерий χ² может называться как критерием согласия, так и критерием независимости, критерием однородности. Закон распределения χ² (хи–квадрат) открыл К. Пирсон. Кривая распределения, полученная из функции хи–квадрат:

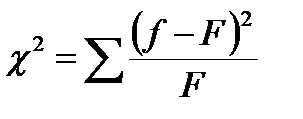(5.4)

где f – фактические и F – теоретические частоты численности объектов выборки. Ее вид в сильной степени зависит от числа степеней свободы. Для малого числа степеней свободы ν кривая асимметрична (рисунок 5.3), но с увеличением ν асимметрия уменьшается и при ν = ∞ кривая становится нормальной гауссовой.

Распределение χ², так же как и t–распределение, частный случай
F – распределения при ν₁ = ν и ν₂ = ∞.

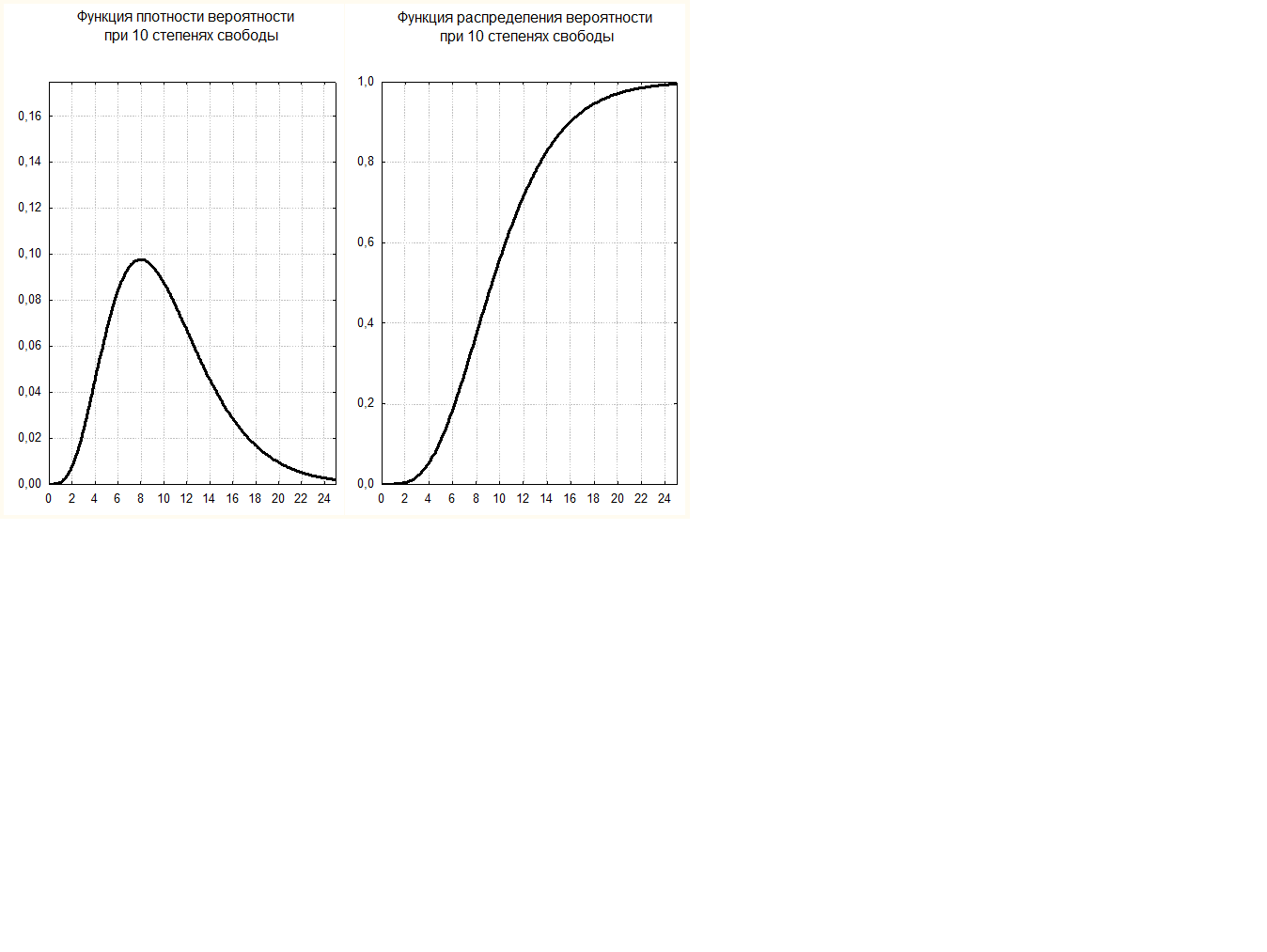
Рисунок 5.3 – Дифференциальное (слева) и интегральное (справа)
χ²–распределение

Вопросы для самоконтроля

1 В каких случаях предпочтительнее использовать t-распределение Стьюдента, а не нормальное распределение?

2 Какие величины необходимо оценивать для использования t-распределения Стьюдента?

3 В чем суть проблемы Беренса–Фишера?

4 Чем численно выражается F-распределение для двух независимых выборок из общей совокупности переменных?

5 От каких характерных величин случайных переменных зависит F-распределение?

6 На какие вопросы может ответить значение критерия χ² при статистической обработке экспериментальных данных?

ТЕМА 6 Основы математической статистики

6.1 Средние величины

6.2 Средняя арифметическая

6.3 Средняя геометрическая

6.4 Средняя гармоническая

Средние величины

Из всех групповых свойств наибольшее теоретическое и практическое значение имеет средний уровень, измеряемый средней величиной признака.

Средняя величина признака – понятие очень глубокое, появившееся в науке и практике только на определенном этапе развития человеческого мышления. Всякая средняя величина обладает тремя основными свойствами: срединным положением, абстрактностью (отвлечение от реально существующего разнообразия) и единством суммарного действия.

Средняя величина признака определяется различными способами в зависимости от объектов наблюдения, изучаемых признаков и целей исследования. Поэтому имеется не одна, а несколько средних: средняя арифметическая, средняя геометрическая, средняя квадратическая, средняя гармоническая, мода, медиана.

Основной показатель – средняя величина – широко используется и в науке, и в практике. При изучении растений, животных, микроорганизмов и человека расчет средних показателей составляет основу обработки первичных материалов.

Средние размеры особей служат для характеристики видов, разновидностей, сортов, пород и других биологических групп; средние показатели физиологических процессов характеризуют интенсивность различных сторон обмена, силу действия биологических агентов и медицинских препаратов.

В производстве средние показатели используются для оценки работы отдельных специалистов, хозяйств, областей.

Средняя величина какого-нибудь признака определяется для того, чтобы получить характеристику этого признака для всей изучаемой группы в целом.

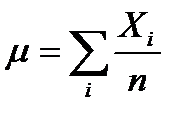(6.1)

В зависимости от объекта наблюдения и от поставленных целей используются в биологии не одна, а несколько средних величин: средняя арифметическая, средняя геометрическая, средняя квадратическая, средняя гармоническая. Кроме того, для характеристики биологических групп иногда употребляются мода и медиана.