Функция распределения и обеспеченности нормального закона распределения

Подставляя в формулу функции распределения (3.15) значение у по формуле (4.18), получаем для нормированного ряда значе­ний

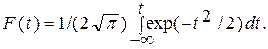(4.22)

Это выражение показывает вероятность того, что случайно вы­бранное значение из нормальной совокупности нормированного ряда меньше значения t, рассчитанного по заданному х.

Расчет вероятности непревышения заданной величины, очевидно, сводится к решению интеграла в правой части формулы (4.22). Этот интеграл не выражается через элементарные функции. Обычно для его вычисления пользуются таблицами специальной функции интеграла вероятностей или функции Лапласа

Ф(Z) = 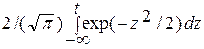(4.23)

Функция F(x) связана с Ф(Z) (см. [64]) следующим соотношением:

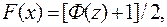(4.24)

где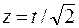

Эта формула может быть использована для непосредственного расчета вероятности непревышения [64] и функции распределения.

Изображение кривой обеспеченности в поле декартовых координат имеет довольно сложные очертания и не дает четкого представления об изменении расходов в области малой и высокой обеспеченности. Поэтому обычно для анализа законов распределения применяют так называемые клетчатки вероятности. Чаще всего используются клетчатки вероятностей для кривых обеспеченности с умеренной асимметричностью. Построение их производится аналитическим или графическим способом [46] таким образом, чтобы кривая обеспеченности нормального закона распределения была линейной.

При использовании формулы расчета функции распределения (4.23) можно рассчитать вероятность попадания случайной вели­чины, подчиняющейся нормальному закону распределения, на за­данный участок значений X от α до β.

Действительно,

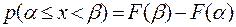(4.25)

Подставляя в это выражение значения F(β) и F (α) по формуле (4.21), получаем

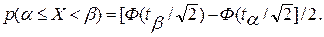(4.26)

Рассчитаем, например, по этой формуле вероятность попадания величины X в интервалы ±σ, ±2σ,±3σ:

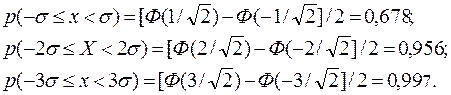(4.27)

Таким образом, если ряд X подчиняется нормальному закону распределения то с вероятностью 67,8 % возможные значения X лежат в пределах ± σ, с вероятность 95,6% в пределах ±2σ и с вероятностью 99,7% в преде­лах ±3σ:

4.4. Распределение ПирсонаIII типа