Уравнение кривой плотности вероятности нормального закона распределения

Если принять F(z)=b_o, то дифференциальное уравнение Пир­сона (4.3) представится в виде

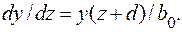
Так как в этом случае принимается, что b₁ = b₂ =.. . = 0, то из системы (4.11) следует, что радиус асимметрии d = 0, а коэффи­циент b_о = - μ₂. Отсюда

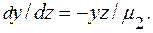(4.12)

Проинтегрировав это выражение, получим

ln y = -z² /(2μ₂ )+C . (4.13)

В точке z = 0 c = ln y. Обозначим значение y при z=0 через y₀. Очевидно, что y₀ будет максимальным значением плотности вероятности, так как при всех других z ln y < ln y₀ . Учитывая это, потенцируем выражение (4.13)

y=y₀ ∙ exp(-z² /(2μ₂ )) (4.14)

Определим теперь максимальное значение y₀ , исходя из ранее установленого соотношения( 3.17). Подставив в формулу (3.17) значение y по формуле (4.14) получаем

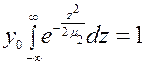(4.15)

Обозначим

t=z/ (2μ₂)^0,5

или учитывая, что μ₂=D_z = σ_z²,

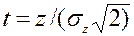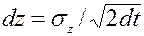и (4.16)

Подставив значения t и dz в формулу (4.15) , после несложных преобразований, используя интеграл Эйлера-Пуассона, получим

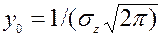(4.17)

Наконец, подставив значение y₀ в формулу (4.14) получим общий вид уравнения нормальной кривой распределения

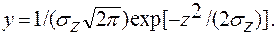(4.18)

Так как z — значение исходного ряда X в отклонениях модульных коэффициентов от единицы (см. разд. 4.2), то σ_z = C_v и

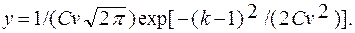(4.19)

В соответствии с этим для исходного ряда X

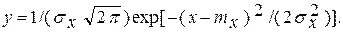(4.20)

Как следует из полученного выражения плотность распределения нормального закона, а следовательно и функция распределения у зависит от двух параметров: т_х, σ_х,. Значение с_s = 0.

Если вместо значений X взять значения нормированной случайной величины (см. разд. 3.1.4), то, учитывая, что σ_t=1 (см. раздел 3.1.6. ), получаем

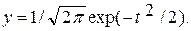(4.21)

Здесь плотность вероятности у зависит уже только от одного аргумента t. Эта зависимость может быть представлена в компактной табличной форме [64). По этой таблице производится расчет кривой плотности веро­ятности для любого исходного ряда X, подчиняющегося нормальному закону распределения. Переход от нормированных значений ординат к исходным выполняется в соответствии с выражением (3.53)

Впервые нормальный закон распределения был разработан для анализа погрешностей измерений. На этой основе он и получил наибольшее распространение во многих отраслях науки и техники, в том числе в геоэкологии где он широко используется для оценки точности расчетов, определения доверительных интервалов и т. д. Следует также отметить, что методы оценки параметров нормального закона распределения хорошо разработаны и доступны. Для его применения достаточно знать два параметра: т_х и σ_x. Поэтому в практических исследованиях иногда допускается, что при описании некоторых рядов, имеющих асимметричное распределение, без особого ущерба может использоваться нормальное распределение. Однако погрешность вследствие ошибочно принятого допущения о нормальности распределения будет различной в каждом конкретном случае. Многие статистические методы, раз­работанные при этом допущении, остаются справедливыми в слу­чае умеренных отклонений от него, например, дисперсионный ана­лиз. В других методах, особенно при корреляционном анализе, это допущение может привести к серьезным погрешностям.