Биномиальное распределение

Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины.

Если результатом испытания является случайное событие, принимающее числовое значение, то говорят о случайной величине.

Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.

Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной. Примеры: число очков, выпавших при бросании игральной кости; число родившихся детей в семье; число шаров, которые можно достать из урны и т. д.

Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной случайной величиной.

Примеры: прирост веса домашнего животного за месяц есть случайная величина, которая может принять значение из некоторого промежутка; прогнозируемая температура воздуха по области и т. д.

Закон распределения случайной величины

где x₁, x₂, …, x_n - случайные величины, соответствующие полной группе событий, т. е. p₁ + p₂ + … + p_n = 1.

При возрастании количества исходов полной группы событий закон распределения становится менее наглядным, и оценить наиболее вероятный исход становится достаточно трудно. Поэтому вводят характеристики случайных величин: математическое ожидание - ожидаемая величина в данном опыте, дисперсия - разброс значений.

Некоторые законы распределения

Биномиальное распределение

Пусть производится n испытаний, причем вероятность появления события А в каждом испытании равна р и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события А в одном испытании равна р, то вероятность его ненаступления равна q = 1 - р.

Найдем вероятность того, что при n испытаниях событие А наступит m раз (m < n). Пусть событие А наступило в первых n испытаниях m раз и не наступило во всех последующих испытаниях. Это сложное событие можно написать в виде произведения:

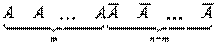
Общее число сложных событий, в которых событие А наступает т раз, равно числу сочетаний из n элементов по m элементов. Так как эти сложные события несовместимы, то вероятность их суммы равна сумме вероятностей. При этом вероятность каждого сложного события равна pm Ч qn-m. Вероятность появления события А m раз в n испытаниях равна:

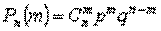
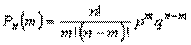(формула Бернулли).

Закон биномиального распределения