Распределение Гумбела
В практике расчетов экстремальных значений гидрометеорологических характеристик различной вероятности превышения широкое распространение за рубежом (главным образом в США и Франции) получили кривые обеспеченности Гумбела, основанные на законах распределения крайних членов выборки [15].
Пусть, например, имеется ряд наблюдений за стоком за п лет, представленный в виде последовательности ежедневных расходов. Тогда ежедневные расходы х1i, х2i, . .., xni в каждом i –м году можно принять за последовательность значений случайной величины Хi. Как и каждая случайная величина, величина Xi может быть описана функцией распределения
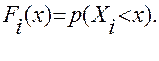 (4.76)
(4.76)
Предположим, что распределение стока в каждом году одинаково и описывается показательным законом
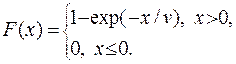
 (4.77)
(4.77)
Можно показать, что в приведенной формуле v равно математическому ожиданию [50, 64].
Рассмотрим теперь событие, состоящее в том, что какое-то значение X, равное ип, не будет превышено в течение п лет, т. е. Un ≥ max (X1, X2, . .., Хп). Тогда очевидно, что Un < x одновременно означает, что Х1 < х, Х2 < х, .. ., Хп <х, т. е. данное значение х больше, чем экстремальное значение за весь период наблюдений. Отсюда, по правилу умножения вероятностей независимых событий, вероятность не превышения р(Uп<.х) или иначе функция распределения может быть определена по формуле
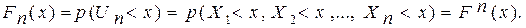 (4.78)
(4.78)
или с учетом формулы (4.77),
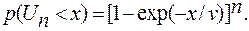 (4.79)
(4.79)
Mожно доказать, что среднее значение Un должно расти с ростом п, будучи равным [50]
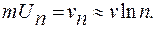 (4.80)
(4.80)
Представим значение X в отклонениях от mUn, т. е.
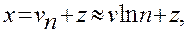 (4.81)
(4.81)
где z — отклонение от тUn любого знака.
Тогда
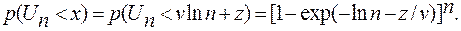 (4.82)
(4.82)
или, так как 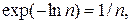 то
то
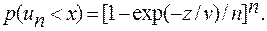 (4.83)
(4.83)
Как известно, при n → ∞ (1 – u/n)n= exp (-u). Отсюда, при том же условии,
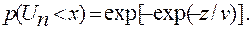 (4.84)
(4.84)
Полученный закон распределения максимальных значений X — Un называется двойным показательным законом распределения. Общий вид этого закона
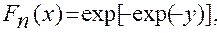 (4.85)
(4.85)
где у = z/v — представляет собой нормированное отклонение от моды.
По формуле (4.84) рассчитаны значения Fn (x) для различных значений у
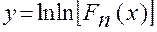 . (4.86)
. (4.86)
В свою очередь по значениям Fn(x) при различных значениях рассчитаны координаты функции обеспеченности Рп(х) =1— Fn(x)
Таблица 4.1
Значения функции Рп(х) при различных значениях y
| y | Pn | y | Pn | y | Pn | y | Pn | y | Pn |
| 9,10 | 0,01 | 4,00 | 1,80 | 1,50 | 20,0 | 0,09 | -1,00 | ||
| 6,90 | 0,12 | 3,49 | 3,00 | 1.25 | 25,0 | 0.00 | -1,10 | ||
| 6,00 | 0,24 | 3,00 | 4,90 | 1,03 | 30,0 | -0,19 | -1,53 | ||
| 5,30 | 0,50 | 2,97 | 5,00 | 1,00 | 31,0 | -0,27 | -1,93 | 99.9 | |
| 5,00 | 0,67 | 2,25 | 10,0 | 0,67 | 40,0 | -0,48 | -2,00 | 99,94 | |
| 4,60 | 1,00 | 2,00 | 13,0 | 0,37 | 50,0 | -0,83 |
Связь значений у и х определяется по уравнению прямой линии
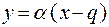 . (4.87)
. (4.87)
В этом уравнении
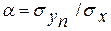 , (4.88)
, (4.88)
где σуп — среднее квадратическое отклонение значений у при данном объеме выборки п, σх— среднее квадратическое отклонение исходного ряда X.
Значение q при известном значении α может быть рассчитано по формуле
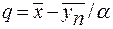 , (4.89)
, (4.89)
где 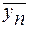 и
и 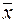 – среднее значение ряда Y и X.
– среднее значение ряда Y и X.
Для расчета значений 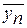 и
и 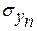 рассчитываются координаты эмпирической кривой обеспеченности по формуле (3.89) и по формуле (4.85) или по таблице y = f(P) определяется последовательность значений у1, y2, ..., уп. По полученной последовательности рассчитываются среднее
рассчитываются координаты эмпирической кривой обеспеченности по формуле (3.89) и по формуле (4.85) или по таблице y = f(P) определяется последовательность значений у1, y2, ..., уп. По полученной последовательности рассчитываются среднее 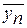 и среднее квадратическое отклонение
и среднее квадратическое отклонение 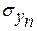 . Очевидно, что
. Очевидно, что 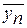 = f(n) и
= f(n) и 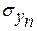 = fn. Имеются специальные таблицы этих зависимостей ( [63], табл. 12).
= fn. Имеются специальные таблицы этих зависимостей ( [63], табл. 12).
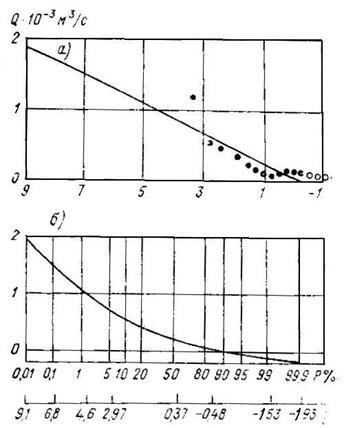
Рис. 4.4. Кривая обеспеченности Гумбела в поле декартовых координат (а) и клетчатки вероятности (б).
Для практического применения метода Гумбела используется процедура, приводящая к построению графика зависимости исследуемых максимальных величин (например, максимальные расходы) от нормированных отклонений от моды у. При этом совокупность точек, отвечающих на графике имеющимся наблюдениям, аппроксимируется в поле декартовых координат прямой линией, по которой и производится экстраполяция значений максимального стока до значений, отвечающих заданной вероятности. Уравнение теоретической прямой, согласно вышеизложенному, принимается в виде
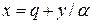 . (4.90)
. (4.90)
а оценка эмпирической обеспеченности производится по формуле (3.70).
В практике кривые обеспеченности Гумбела строятся в поле клетчатки вероятности для кривых с умеренной асимметричностью по следующей схеме:
1. По соответствующим значениям у и Р (табл.4.1) параллельно и ниже оси абсцисс строится шкала значений у (рис. 4.5);
2. Члены исходного ряда X располагаются в убывающем порядке, и по формуле (3.89) рассчитываются их эмпирические обеспеченности. Рассчитанные эмпирические точки (xi, Pi) наносятся в поле клетчатки вероятности. Очевидно, что в отличие от эмпирической кривой обеспеченности в декартовых координатах (по оси абсцисс y = f(P), по оси ординат — х), здесь, при Cs≠0,. кривая обеспеченности будет иметь вид кривой линии;
3. По формулам (3.20) и (3.31) рассчитывается среднее арифметическое значение Х и среднее квадратическое отклонение σх;
4. По таблице 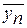 , σy=f(n) [64] по числу членов исходного ряда определяется среднее значение
, σy=f(n) [64] по числу членов исходного ряда определяется среднее значение 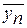 и среднее квадратичное отклонение
и среднее квадратичное отклонение 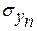 ;
;
5. По формулам (4.87) и (4.88) определяются коэффициенты уравнения α и q;
6. Значения а и q подставляются в уравнение (4.89), и по различным значениям у рассчитываются значения х;
7. Значения х = f(у) наносятся на клетчатку вероятностей, причем в качестве абсциссы принимается ранее построенная ось (см. рис. 4.5).
8. Вид дифференциальных и интегральных кривых распределения Гумбела представлен на рис. 4.6, Очевидно, что кривая распределения одномодальна, мода распределения находится в точке x = q. Значение у в этой точке равно нулю, а плотность распределения, как следует из формулы (4.84), равна 0,37. При достаточно большом п (п→∞) значения 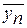 и σу стремятся к пределу соответственно 0,86 и 1,28.
и σу стремятся к пределу соответственно 0,86 и 1,28.
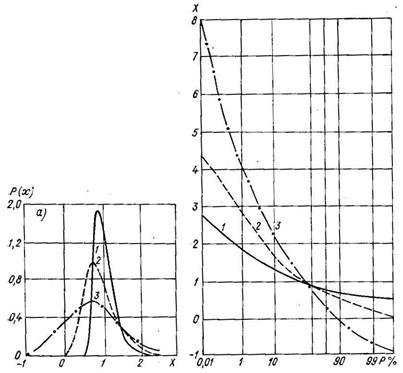
Рис. 4.6. Влияние Сv на форму кривой распределения (а) и кривой обеспеченности (б) Гумбела. (1 – Сv = 0,25, 2 – Сv = 0,50, 3 – Сv = 1,0)
Параметры более высокого порядка для рассматриваемого расределения постоянны: коэффициент асимметрии Сs=1,14, эксцесс E = 2,40. Таким образом, распределение Гумбела является двухпараметрическим.
При использовании кривых обеспеченности Гумбела для расчетов экстремальных значений стока и других гидрометеорологических характеристик необходимо иметь ввиду, что при выводе формулы функции распределения были приняты следующие допущения.
1. Отдельные значения каждой случайной величины Xi (i =1, 2, ..., п) взаимно независимы. При расчетах стока это равносильно утверждению о том, что суточные расходы воды в каждом году взаимно независимы.
2. Функции распределения суточных значений стока в каждом году одинаковы и имеют экспоненциальный характер.
3. Число элементов выборки значений каждой случайной величины Xi для применения асимптотической теории достаточно велико.
Указанные допущения, принимаемые при применении функции распределения Гумбела для рядов значений гидрометеорологических процессов, вряд ли можно считать с физической точки зрения достаточно обоснованными. Например, при расчете максимального стока утверждение о независимости ежедневных расходов внутри года явно не соответствует фактическим данным, подтверждающим наличие достаточно высокой корреляции. Одним из следствий наличия высокой внутрирядной корреляции между суточными расходами воды является уменьшение объема независимой информации, которая может быть гораздо меньше, чем число дней в году, а следовательно и недостаточна для утверждения об асимптотическом приближении. Приближенным является также утверждение об одинаковом распределении расходов в каждом году.
Наконец из теоретического анализа, выполненного Г. А. Алексеевым [4], следует, что предельное значение третьего центрального момента µ3 для кривой распределения наибольшего члена, выборки при п→∞ равно 2,40, отсюда Csy =μ3/σy3 —1,14.
Более детально отмеченные свойства кривой Гумбела на ряде примеров рассмотрены в работе [52].
Дата добавления: 2020-10-25; просмотров: 853;











